算法设计与分析-动态规划区间DP题目记录。
区间DP&其他 301 独立任务最优调度问题 问题描述 用两台处理机A和B处理n个作业,每个机器处理第i个作业所需的时间分别为和,某些作业在机器A上作业更快,有些作业在机器B上工作更快,每台机器都不能同时处理两个作业。对于给定的2台处理机A和B处理n个作业,找出一个最优调度方案,使两台机器处理完n个作业的时间最短。
输入格式: 第一行是一个正整数n,表示处理n个作业。接下来的2行中,每行n个正整数,表示A和B处理第i个作业的时间。
算法设计 子问题分解:定义t[i][j]为:表示完成i个作业且机器A花费j时间的情况下,机器B所花费时间的最小值。第i件作业如果由机器A处理,则t[i][j] = t[i - 1][j - a[i]],如果由机器B处理,则t[i][j] = t[i - 1][j] + b[i],因此t[i][j] = min{t[i - 1][j] + b[i], t[i - 1][j - a[i]]}。
递推方程:
代码实现 C++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 #include <iostream> #include <climits> #include <cstring> #include <cmath> using namespace std;const int MAXT = 10000 ;int solution (int n, int *a, int *b) int t[n+1 ][MAXT], max_t , min_t ; memset (t, 0 , sizeof (t)); max_t = 0 ; for (int i=1 ;i<=n;i++){ max_t += a[i]; } for (int i=1 ;i<=n;i++){ for (int j=0 ;j<=max_t ;j++){ if (j<a[i]){ t[i][j] = t[i-1 ][j] + b[i]; } else { t[i][j] = min (t[i-1 ][j-a[i]], t[i-1 ][j] + b[i]); } } } min_t = INT_MAX; for (int i=0 ;i<=max_t ;i++){ min_t = min (max (t[n][i], i), min_t ); } return min_t ; } int main () int n, *a, *b, result; cin>>n; a = new int [n+1 ]; b = new int [n+1 ]; for (int i=1 ;i<=n;i++){ cin>>a[i]; } for (int i=1 ;i<=n;i++){ cin>>b[i]; } result = solution (n, a, b); cout << "result = " << result; delete [] a; delete [] b; return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 import java.util.Scanner; import java.lang.Math;public class DP301 { public static void main (String[] args) { int n, result; int [] a,b; Scanner s = new Scanner (System.in); n = s.nextInt(); a = new int [n+1 ]; b = new int [n+1 ]; for (int i=1 ;i<=n;i=i+1 ){ a[i] = (int ) s.nextInt(); } for (int i=1 ;i<=n;i=i+1 ){ b[i] = (int ) s.nextInt(); } result = solution(n, a, b); System.out.println("result=" +result); } public static int solution (int n, int [] a, int [] b) { int [][] t = new int [n+1 ][10000 ]; int max_t, min_t; max_t = 0 ; for (int i=1 ;i<=n;i++){ max_t += a[i]; } for (int i=1 ;i<=n;i++){ for (int j=0 ;j<=max_t;j++){ if (j<a[i]){ t[i][j] = t[i-1 ][j] + b[i]; } else { t[i][j] = Math.min(t[i-1 ][j-a[i]], t[i-1 ][j] + b[i]); } } } min_t = Integer.MAX_VALUE; for (int i=0 ;i<=max_t;i++){ min_t = Math.min(Math.max(t[n][i], i), min_t); } return min_t; } }
测试输入与输出 输入:
6
2 5 7 10 5 2
3 8 4 11 3 4
输出:
15
303 石子合并问题 问题描述 在一个圆形操场的四周摆放着n堆石子。现要将石子有次序的合并成一堆。规定每次只能选相邻的石子合并成一堆,并将新的一堆石子数即为该次合并的得分。试设计一个算法,计算出将n堆石子合并成一堆的最小得分和最大得分。输入为n和每堆石子的数量。
输入格式 第一行是正整数n,表示n堆石子。第2行有n个数,表示每堆石子的个数。
算法设计 先考虑石子直线摆放的情况。假设将石子合并记为S[i:j]。考虑计算S[1:n]的合并方法,假设S[1:n]的最优合并方法在k堆石子处断开,则合并方式为,合并得分为S[1:k]的得分加上S[k+1:n]的合并得分,再加上这两堆石子的得分。这个问题的最优子结构在于,如果S[1:n]合并方法是最优的,那么S[1:k]和S[k+1:n]的合并也是最优的。
用a[i]表示前i堆石子的数量,m[i][j]表示合并第i到j堆的最小合并得分。递推方程可写为:
对于环形摆放,只要将石子按顺序放到原来石子堆顺序的尾部就可以实现首尾相连了,例如石子堆4 4 5 9,扩展为石子堆4 4 5 9 4 4 5 9,就能将首尾相连的环形情况包括进去,最后的结果是m[1][4],m[2][5],m[3][6],m[4][7]中的最值。
算法实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 #include <iostream> #include <climits> #include <cstring> #include <cmath> using namespace std;void solution (int n, int *stones) int a[2 *n+1 ], stones_line[2 *n+1 ], m_min[2 *n+1 ][2 *n+1 ], m_max[2 *n+1 ][2 *n+1 ]; memset (a, 0 , sizeof (a)); memset (m_min, 0 , sizeof (m_min)); memset (m_max, 0 , sizeof (m_max)); for (int i=n+1 ;i<=2 *n;i++){ stones_line[i-n] = stones_line[i] = stones[i-n]; } for (int i=1 ;i<=2 *n;i++){ a[i] = a[i-1 ] + stones_line[i]; } for (int r=2 ;r<=n;r++){ for (int i=1 ;i<=2 *n-r+1 ;i++){ int j = i + r - 1 ; m_min[i][j] = INT_MAX; m_max[i][j] = INT_MIN; for (int k=i;k<j;k++){ m_min[i][j] = min (m_min[i][j], m_min[i][k]+m_min[k+1 ][j]+a[j]-a[i-1 ]); m_max[i][j] = max (m_max[i][j], m_max[i][k]+m_max[k+1 ][j]+a[j]-a[i-1 ]); } } } int min_score, max_score; min_score = INT_MAX; max_score = INT_MIN; for (int i=1 ;i<=n;i++){ min_score = min (min_score, m_min[i][i+n-1 ]); max_score = max (max_score, m_max[i][i+n-1 ]); } cout << "min_score = " << min_score << endl << "max_score = " << max_score << endl ; } int main () int n; cin >> n; int stones[n+1 ]; for (int i=1 ;i<=n;i++){ cin >> stones[i]; } solution (n, stones); return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 import java.util.Scanner;import java.lang.Math;public class DP303 { public static void main (String args[]) { int n; int [] stones; Scanner sc = new Scanner (System.in); n = sc.nextInt(); stones = new int [n+1 ]; for (int i=1 ;i<=n;i++){ stones[i] = sc.nextInt(); } solution(n, stones); } public static void solution (int n, int [] stones) { int [] a, stones_line; int [][] m_min, m_max; a = new int [2 *n+1 ]; stones_line = new int [2 *n+1 ]; m_min = new int [2 *n+1 ][2 *n+1 ]; m_max = new int [2 *n+1 ][2 *n+1 ]; for (int i=n+1 ;i<=2 *n;i++){ stones_line[i] = stones_line[i-n] = stones[i-n]; } for (int i=1 ;i<=2 *n;i++){ a[i] = a[i-1 ] + stones_line[i]; } for (int r=2 ;r<=n;r++){ for (int i=1 ;i<=2 *n-r+1 ;i++){ int j = i + r - 1 ; m_min[i][j] = Integer.MAX_VALUE; m_max[i][j] = Integer.MIN_VALUE; for (int k=i;k<j;k++){ m_min[i][j] = Math.min(m_min[i][j], m_min[i][k]+m_min[k+1 ][j]+a[j]-a[i-1 ]); m_max[i][j] = Math.max(m_max[i][j], m_max[i][k]+m_max[k+1 ][j]+a[j]-a[i-1 ]); } } } int min_score, max_score; min_score = Integer.MAX_VALUE; max_score = Integer.MIN_VALUE; for (int i=1 ;i<=n;i++){ min_score = Math.min(min_score, m_min[i][i+n-1 ]); max_score = Math.max(max_score, m_max[i][i+n-1 ]); } System.out.printf("min_score = %d\n" , min_score); System.out.printf("max_score = %d" , max_score); } }
测试输入与输出 输入:
4
4 4 5 9
输出:
43
54
304 数字三角形问题 问题描述 给定一个由n行数字组成的数字三角形,试设计一个算法,计算出从三角形的顶至底的一条路径,使该路径经过的数字总和最大。
输入格式 第一行为n,后n行为三角形的元素。
算法设计 设dp[i][j]表示从顶层开始第i层的第j个元素为最后一个元素的路径的数字和最大值,t[i][j]表示第i层i个数字,可得递推方程如下:
最大的路径上数字和为
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 # include <iostream> # include <cmath> using namespace std;void solution (int n, int **t) int dp[n+1 ][n+1 ]; dp[2 ][1 ] = t[1 ][1 ] + t[2 ][1 ]; dp[2 ][2 ] = t[1 ][1 ] + t[2 ][2 ]; for (int i=3 ;i<=n;i++){ dp[i][1 ] = dp[i-1 ][1 ] + t[i][1 ]; dp[i][i] = dp[i-1 ][i-1 ] + t[i][i]; for (int j=2 ;j<i;j++){ dp[i][j] = max (dp[i-1 ][j-1 ], dp[i-1 ][j]) + t[i][j]; } } int res = -1 ; for (int i=1 ;i<=n;i++){ res = max (dp[n][i], res); } cout << res << endl; } int main () int n; cin>>n; int **t; t = new int *[n+1 ]; for (int i=1 ;i<=n;i++){ t[i] = new int [n+1 ]; } for (int i=1 ;i<=n;i++){ for (int j=1 ;j<=i;j++){ cin>>t[i][j]; } } solution (n, t); for (int i=1 ;i<=n;i++){ delete [] t[i]; } delete [] t; return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 import java.util.Scanner;import java.lang.Math;public class DP304 { public static void main (String[] args) { Scanner sc = new Scanner (System.in); int n = sc.nextInt(); int [][] t = new int [n+1 ][n+1 ]; for (int i=1 ;i<=n;i++){ for (int j=1 ;j<=i;j++){ t[i][j] = sc.nextInt(); } } solution(n, t); } public static void solution (int n, int [][] t) { int [][] dp = new int [n+1 ][n+1 ]; dp[2 ][1 ] = t[1 ][1 ] + t[2 ][1 ]; dp[2 ][2 ] = t[1 ][1 ] + t[2 ][2 ]; for (int i=3 ;i<=n;i++){ dp[i][1 ] = dp[i-1 ][1 ] + t[i][1 ]; dp[i][i] = dp[i-1 ][i-1 ] + t[i][i]; for (int j=2 ;j<i;j++){ dp[i][j] = Math.max(dp[i-1 ][j-1 ], dp[i-1 ][j]) + t[i][j]; } } int res = -1 ; for (int i=1 ;i<=n;i++){ res = Math.max(dp[n][i], res); } System.out.println(res); } } public static void solution (int n, int [][] t) { int [][] dp = new int [n+1 ][n+1 ]; dp[2 ][1 ] = t[1 ][1 ] + t[2 ][1 ]; dp[2 ][2 ] = t[1 ][1 ] + t[2 ][2 ]; for (int i=3 ;i<=n;i++){ dp[i][1 ] = dp[i-1 ][1 ] + t[i][1 ]; dp[i][i] = dp[i-1 ][i-1 ] + t[i][i]; for (int j=2 ;j<i;j++){ dp[i][j] = Math.max(dp[i-1 ][j-1 ], dp[i-1 ][j]) + t[i][j]; } } int res = -1 ; for (int i=1 ;i<=n;i++){ res = Math.max(dp[n][i], res); } System.out.println(res); }
测试输入与输出 输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出:
30
305乘法表问题 问题描述 定义字母表{a,b,c}上的乘法表如下:
a
b
c
a
b
b
a
b
c
b
a
c
a
c
c
依次乘法表,对于任一定义于该字母表上的字符串,适当加括号后,得到一个表达式。例如x=bbbba。一个加括号方式为(b(bb))(ba),结果为a。设计一个动态规划算法,计算有多少种不同的方式,使由字符串x导出的加括号表达式结果为a。
输入格式 输入为给定字符串。
算法设计 可以将每种加括号方式下得到一个字符的方式都记录下来,最后计算出结果为a的方式。假设用dp[i][j][c]表示从i乘到j,得到字符c的方法数,计算dp[i][j][c]时,需要考虑每一种断开,假设从k处断开,则方法数为∑ dp[i][k][c1]*dp[k+1][j][c2],c1*c2 = c。最终得到dp[1][n][a]即为所求结果。
递推方程如下:
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <iostream> #include <cstring> using namespace std;void solution (char c[]) int n = strlen (c); int dp[n+1 ][n+1 ][3 ]; memset (dp, 0 , sizeof (dp)); for (int i=1 ;i<=n;i++){ if (c[i-1 ]=='a' ) dp[i][i][0 ] = 1 ; else if (c[i-1 ]=='b' ) dp[i][i][1 ] = 1 ; else if (c[i-1 ]=='c' ) dp[i][i][2 ] = 1 ; } for (int r=2 ;r<=n;r++){ for (int i=1 ;i<=n-r+1 ;i++){ int j = i + r - 1 ; for (int k=i;k<j;k++){ dp[i][j][0 ] += dp[i][k][0 ]*dp[k+1 ][j][2 ] + dp[i][k][1 ]*dp[k+1 ][j][2 ] + dp[i][k][2 ]*dp[k+1 ][j][0 ]; dp[i][j][1 ] += dp[i][k][0 ]*dp[k+1 ][j][0 ] + dp[i][k][0 ]*dp[k+1 ][j][1 ] + dp[i][k][1 ]*dp[k+1 ][j][1 ]; dp[i][j][2 ] += dp[i][k][1 ]*dp[k+1 ][j][0 ] + dp[i][k][2 ]*dp[k+1 ][j][1 ] + dp[i][k][2 ]*dp[k+1 ][j][2 ]; } } } cout << dp[1 ][n][0 ]; } int main () char c[1024 ]; cin >> c; solution (c); return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import java.util.Scanner;public class DP305 { public static void main (String[] args) { solution(args[0 ]); } public static void solution (String c) { int n = c.length(); int [][][] dp = new int [n+1 ][n+1 ][3 ]; for (int i=1 ;i<=n;i++){ if (c.charAt(i-1 )=='a' ) dp[i][i][0 ] = 1 ; else if (c.charAt(i-1 )=='b' ) dp[i][i][1 ] = 1 ; else if (c.charAt(i-1 )=='c' ) dp[i][i][2 ] = 1 ; } for (int r=2 ;r<=n;r++){ for (int i=1 ;i<=n-r+1 ;i++){ int j = i + r - 1 ; for (int k=i;k<j;k++){ dp[i][j][0 ] += dp[i][k][0 ]*dp[k+1 ][j][2 ] + dp[i][k][1 ]*dp[k+1 ][j][2 ] + dp[i][k][2 ]*dp[k+1 ][j][0 ]; dp[i][j][1 ] += dp[i][k][0 ]*dp[k+1 ][j][0 ] + dp[i][k][0 ]*dp[k+1 ][j][1 ] + dp[i][k][1 ]*dp[k+1 ][j][1 ]; dp[i][j][2 ] += dp[i][k][1 ]*dp[k+1 ][j][0 ] + dp[i][k][2 ]*dp[k+1 ][j][1 ] + dp[i][k][2 ]*dp[k+1 ][j][2 ]; } } } System.out.println(dp[1 ][n][0 ]); } }
测试输入与输出 输入:
bbbba
输出:
6
306 租用游艇问题 问题描述 在长江上有n个游艇出租站1,2,…,n。游客可在任何出租站租用游艇,并在下游的任何一个出租站归还游艇。出租站i到出租站j之间的租金为r(i,j)。使设计一个算法,计算从出租站1到出租站n所需的最少租金。
输入格式 第一行的正整数n表示有n个出租站,此后的n-1行为r(i,j),i和j取1-n,i<j。
算法设计 假设dp[i][j]表示从出租站i到出租站j的租金,从i到j可以在中间的第k个站归还并重新租借游艇,则dp[i][j]= dp[i][k]+dp[k][j],递推方程为:
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <iostream> #include <cmath> #include <cstring> using namespace std;void solution (int n, int **r) int dp[n+1 ][n+1 ]; memset (dp, 0 , sizeof (dp)); for (int rr=2 ;rr<=n;rr++){ for (int i=1 ;i<=n-rr+1 ;i++){ int j = i + rr - 1 ; dp[i][j] = r[i][j]; for (int k=i;k<j;k++){ dp[i][j] = min (dp[i][j], dp[i][k]+dp[k][j]); } } } cout << dp[1 ][n] << endl; } int main () int n, **r; cin >> n; r = new int *[n+1 ]; for (int i=1 ;i<=n;i++){ r[i] = new int [n+1 ]; } for (int i=1 ;i<=n;i++){ for (int j=i+1 ;j<=n;j++){ cin >> r[i][j]; } } solution (n, r); for (int i=1 ;i<=n;i++){ delete [] r[i]; } delete [] r; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 import java.util.Scanner;public class DP306 { public static void main (String args[]) { int n; Scanner sc = new Scanner (System.in); n = sc.nextInt(); int [][] r = new int [n+1 ][n+1 ]; for (int i=1 ;i<=n;i++){ for (int j=i+1 ;j<=n;j++){ r[i][j] = sc.nextInt(); } } solution(n, r); } public static void solution (int n, int [][] r) { int [][] dp = new int [n+1 ][n+1 ]; for (int rr=2 ;rr<=n;rr++){ for (int i=1 ;i<=n-rr+1 ;i++){ int j = i + rr - 1 ; dp[i][j] = r[i][j]; for (int k=i;k<j;k++){ dp[i][j] = Math.min(dp[i][j], dp[i][k]+dp[k][j]); } } } System.out.println(dp[1 ][n]); } }
测试输入与输出 输入:
3
5 15
7
输出:
12
308 最小m段和 有一个n个数形成的整数序列,将该序列划分为m段,每段求和,求子段和的最大值。设计一个动态规划算法,找出使子段和的最大值的最小值。
输入格式 第一行有两个正整数n和m,n是序列长度,m是段数。第二行有n个整数,是序列的元素值。
算法设计 设dp[i][j]表示将前i项划分为j个子段后,子段和的最大值的最小值,所求最优值为dp[n][m]。考虑不同的划分方法,当j=1时,,当j>1时,假设在前k项中有j-1个子段,后i-k+1项为1个子段,则这种划分方式下的最大子段和为,或者在前j-1段,或者在最后一段。要找到一个k,使这个最大值最小,因此递推方程如下:
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <iostream> #include <cmath> #include <cstring> #include <climits> using namespace std;void solution (int n, int m, int a[]) int dp[n+1 ][n+1 ]; memset (dp, 0 , sizeof (dp)); for (int i=1 ;i<=n;i++){ dp[i][1 ] = dp[i-1 ][1 ] + a[i]; } for (int i=1 ;i<=n;i++){ for (int j=2 ;j<=3 ;j++){ dp[i][j] = INT_MAX; for (int k=j-1 ;k<=i;k++){ int t = max (dp[k][j-1 ], dp[i][1 ] - dp[k][1 ]); dp[i][j] = min (t, dp[i][j]); } } } cout << dp[n][m] << endl; } int main () int n, m; cin >> n >> m; int a[n+1 ]; for (int i=1 ;i<=n;i++){ cin >> a[i]; } solution (n, m , a); return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 import java.util.Scanner;public class DP308 { public static void main (String args[]) { int n,m; Scanner sc = new Scanner (System.in); n = sc.nextInt(); m = sc.nextInt(); int [] a = new int [n+1 ]; for (int i=1 ;i<=n;i++){ a[i] = sc.nextInt(); } solution(n, m , a); } public static void solution (int n, int m, int [] a) { int [][] dp = new int [n+1 ][n+1 ]; for (int i=1 ;i<=n;i++){ dp[i][1 ] = dp[i-1 ][1 ] + a[i]; } for (int i=1 ;i<=n;i++){ for (int j=2 ;j<=3 ;j++){ dp[i][j] = Integer.MAX_VALUE; for (int k=j-1 ;k<=i;k++){ int t = Math.max(dp[k][j-1 ], dp[i][1 ] - dp[k][1 ]); dp[i][j] = Math.min(t, dp[i][j]); } } } System.out.println(dp[n][m]); } }
测试输入与输出 输入:
5 3
5 4 3 2 1
输出:
6
310 最大长方体问题 问题描述 一个长,宽,高分别为m,n,p的长方体被分隔为mxnxp个小立方体,每个小立方体内有一个整数,设计一个算法,计算所给长方体的最大子长方体,子长方体的大小定义为所含整数之和。
输入格式 第一行的三个整数为m,n,p。接下来的mxn行每行p个整数,表示小立方体的数。
算法设计 假设原问题为对一个条形长方体进行切割,则该问题为一个最大子段和问题。假设原问题对一个高度为一的长方体切割,该问题就是最大子段和的二维形式,即最大子矩阵和问题。将原问题的三维形式降维为二维形式,就可以作为最大子矩阵和问题处理,将每个方块的数字保存在dp3[i][j][k]中,i表示长,j表示宽,k表示高,将其降维到二维,再二维降维到一维解决。
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 #include <iostream> #include <cmath> #include <cstring> using namespace std;int maxSum1 (int n, int *a) int maxSum = 0 , sum = 0 ; for (int i=1 ;i<=n;i++){ if (sum>0 ){ sum += a[i]; } else { sum = a[i]; } maxSum = max (maxSum, sum); } return maxSum; } int maxSum2 (int m, int n, int **a) int maxSum = 0 ; int *sum = new int [n+1 ]; for (int i=1 ;i<=m;i++){ memset (sum, 0 , sizeof (int )*(n+1 )); for (int j=i;j<=m;j++){ for (int k=1 ;k<=n;k++){ sum[k] += a[j][k]; } int max1 = maxSum1 (n, sum); maxSum = max (max1, maxSum); } } delete [] sum; return maxSum; } int maxSum3 (int m, int n, int p, int ***a) int maxSum = 0 ; int **sum = new int *[n+1 ]; for (int i=1 ;i<=n;i++){ sum[i] = new int [p+1 ]; } for (int i=1 ;i<=m;i++){ for (int j=1 ;j<=n;j++){ for (int k=1 ;k<=p;k++){ sum[j][k] = 0 ; } } for (int j=i;j<=m;j++){ for (int k=1 ;k<=n;k++){ for (int h=1 ;h<=p;h++){ sum[k][h] += a[j][k][h]; } } int max2 = maxSum2 (n, p, sum); maxSum = max (max2, maxSum); } } for (int i=1 ;i<=n;i++){ delete [] sum[i]; } delete [] sum; return maxSum; } int main () int m, n, p; cin >> m >> n >> p; int ***a = new int **[m+1 ]; for (int i=1 ;i<=m;i++){ a[i] = new int *[n+1 ]; } for (int i=1 ;i<=m;i++){ for (int j=1 ;j<=n;j++){ a[i][j] = new int [p+1 ]; } } for (int i=1 ;i<=m;i++){ for (int j=1 ;j<=n;j++){ for (int k=1 ;k<=p;k++){ cin >> a[i][j][k]; } } } cout << maxSum3 (m, n, p, a) << endl; for (int i=1 ;i<=m;i++){ for (int j=1 ;j<=n;j++){ delete [] a[i][j]; } } for (int i=1 ;i<=m;i++){ delete [] a[i]; } delete [] a; return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 import java.util.Scanner;import java.util.Arrays;public class DP310 { public static void main (String[] args) { int m, n, p; Scanner sc = new Scanner (System.in); m = sc.nextInt(); n = sc.nextInt(); p = sc.nextInt(); int [][][] a = new int [m+1 ][n+1 ][p+1 ]; for (int i=1 ;i<=m;i++){ for (int j=1 ;j<=n;j++){ for (int k=1 ;k<=p;k++){ a[i][j][k] = sc.nextInt(); } } } System.out.println(maxSum3(m, n, p, a)); } public static int maxSum1 (int n, int [] a) { int maxSum = 0 , sum = 0 ; for (int i=1 ;i<=n;i++){ if (sum>0 ){ sum += a[i]; } else { sum = a[i]; } maxSum = Math.max(maxSum, sum); } return maxSum; } public static int maxSum2 (int m, int n, int [][] a) { int maxSum = 0 ; int [] sum = new int [n+1 ]; for (int i=1 ;i<=m;i++){ Arrays.fill(sum, 0 ); for (int j=i;j<=m;j++){ for (int k=1 ;k<=n;k++){ sum[k] += a[j][k]; } maxSum = Math.max(maxSum, maxSum1(n, sum)); } } return maxSum; } public static int maxSum3 (int m, int n, int p, int [][][] a) { int maxSum = 0 ; int [][] sum = new int [n+1 ][p+1 ]; for (int i=1 ;i<=m;i++){ for (int j=1 ;j<=n;j++){ Arrays.fill(sum[j], 0 ); } for (int j=i;j<=m;j++){ for (int k=1 ;k<=n;k++){ for (int h=1 ;h<=p;h++){ sum[k][h] += a[j][k][h]; } } maxSum = Math.max(maxSum, maxSum2(n, p, sum)); } } return maxSum; } }
测试输入与输出 输入:
3 3 3
0 -1 2
1 2 2
1 1 -2
-2 -1 -1
-3 3 -2
-2 -3 1
-2 3 3
0 1 3
2 1 -3
输出:
14
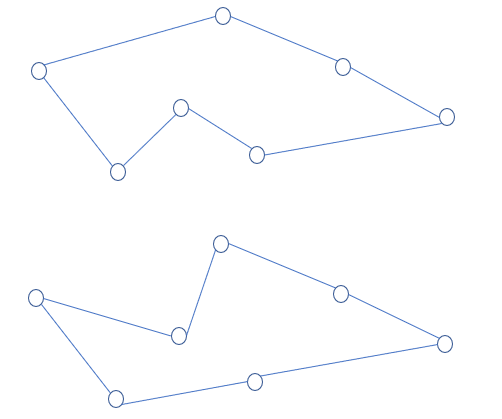
312 双调旅行售货员问题 问题描述 最短双调TSP回路问题是欧式旅行售货员问题的特殊情况。平面上n个点的双调TSP回路是从最左点开始,严格地从左向右直到最右点,然后严格由右至左直到最左点,且连接每个点恰好一次的闭合回路。给定平面上n个点,计算这n个点的最短双调TSP回路。
输入格式 第一行的整数n表示点数,接下来的n行,每行有两个值x和y,表示点的位置。
算法设计 下图是同一个图中,两条不同的双调TSP路径:
由于每个点都要经过一遍,实际上每个点不是在从左到右的路径上,就是在从右到左的路径上,而且如果将所有点按照横坐标进行排序,每次从一个点出发选择下一个点时,从左向右只能选择右侧的点,从右向左只能选择左侧的点。
用d(i,j)表示i点到j点的直线距离,定义dp[i][j]表示从i连接到最左边的点1,点1再连接到最右边的点j的最短距离,dp[i][j]就是原问题的子问题,通过逐步将点加入路径中,最终得到的就是双调TSP回路。
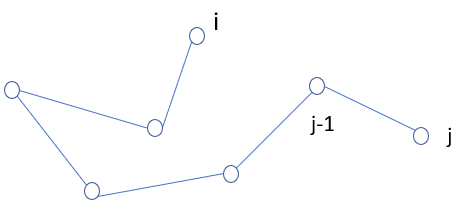
点i在i→1的路径中,点j在1→j的路径中,考虑j左侧的点j-1在哪条路径上:
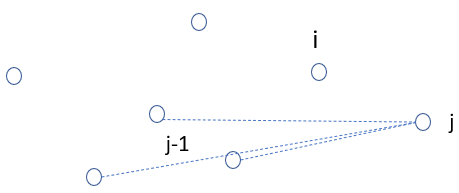
i=j-1,则此时j左侧的第一个点是i,与j相连的路径1→j的点是1 - j-2中的一点k
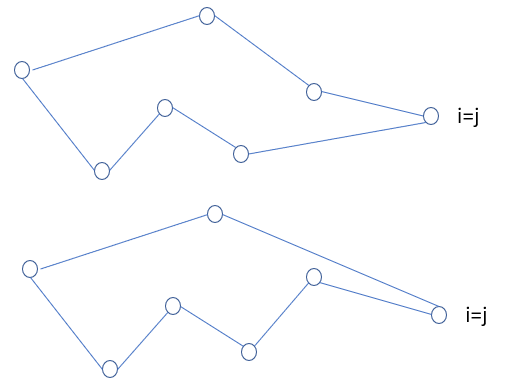
i=j,形成一条回路,此时i=j=n,左侧的点可能是1→n上的,也可能是1←n上的
根据以上三种情况,给出递推方程:
其中,第二种情况是b[k][j-1]而不是b[j-1][k]是因为k<j-1,子问题都是i<j的,因此是b[k][j-1],从k→1→j-1和j-1→1→k的最短路径是一样的。这里用b[k][j-1]表示j-1→1→k的最短距离。
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <iostream> #include <cmath> #include <climits> #include <algorithm> using namespace std;struct point { double x,y; bool operator < (const point &p) const { return x < p.x; } }; double d (point p1, point p2) return sqrt ( pow ((p1.x-p2.x),2 ) + pow ((p1.y-p2.y),2 ) ); } void solution (point p[], int n) double dp[n+1 ][n+1 ]; sort (p+1 , p+n+1 ); dp[1 ][2 ] = d (p[1 ], p[2 ]); for (int j=3 ;j<=n;j++){ for (int i=1 ;i<=j-2 ;i++){ dp[i][j] = dp[i][j-1 ] + d (p[j-1 ], p[j]); } dp[j-1 ][j] = INT_MAX; for (int k=1 ;k<=j-2 ;k++){ dp[j-1 ][j] = min (dp[j-1 ][j], dp[k][j-1 ]+d (p[k],p[j])); } dp[n][n] = dp[n-1 ][n] + d (p[n-1 ], p[n]); } cout << dp[n][n] << endl; } int main () int n; cin >> n; point p[n+1 ]; for (int i=1 ;i<=n;i++){ cin >> p[i].x >> p[i].y; } solution (p, n); return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 import java.util.Scanner;import java.util.Arrays;import java.util.Comparator;class point { public double x,y; public point () {}; public point (double x, double y) { this .x = x; this .y = y;}; } public class DP312 { public static void main (String args[]) { int n; Scanner sc = new Scanner (System.in); n = sc.nextInt(); point[] p = new point [n+1 ]; for (int i=1 ;i<=n;i++){ p[i] = new point (sc.nextDouble(), sc.nextDouble()); } solution(p, n); } public static double d (point p1, point p2) { return Math.sqrt(Math.pow((p1.x-p2.x),2 ) + Math.pow((p1.y-p2.y),2 ) ); } public static void solution (point[] p, int n) { double [][] dp = new double [n+1 ][n+1 ]; Arrays.sort(p, new cmp ()); dp[1 ][2 ] = d(p[1 ], p[2 ]); for (int j=3 ;j<=n;j++){ for (int i=1 ;i<=j-2 ;i++){ dp[i][j] = dp[i][j-1 ] + d(p[j-1 ], p[j]); } dp[j-1 ][j] = Integer.MAX_VALUE; for (int k=1 ;k<=j-2 ;k++){ dp[j-1 ][j] = Math.min(dp[j-1 ][j], dp[k][j-1 ]+d(p[k],p[j])); } dp[n][n] = dp[n-1 ][n] + d(p[n-1 ], p[n]); } System.out.printf("%.2f" , dp[n][n]); } }
测试输入与输出 输入:
7
输出:
25.58
313 最大k乘积问题 问题描述 设I是一个n位十进制整数。如果将I划分为k段,则可得到k个整数。这k个整数的乘积称为I的一个k乘积。设计一个算法,对于给定的I和k,求出I的最大k乘积。
输入格式 第一行的两个整数为n和k,接下来的一行是一个n位十进制整数l。
算法设计 设dp[i][j]表示将前i位划分为j段的最大k乘积,需要找到一个位置m,前m位中有j-1段,此后的位为1段。设a[i][j]表示第i到j位,则
递推方程为:
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <iostream> #include <cmath> #include <cstring> #include <climits> using namespace std;void solution (int n, int k, int num) int a[n+1 ][n+1 ], dp[n+1 ][k+1 ]; for (int i=1 ;i<=n;i++){ for (int j=i;j<=n;j++){ a[i][j] = stoi (to_string (num).substr (i-1 ,j-i+1 )); } } for (int i=1 ;i<=n;i++){ dp[i][1 ] = a[1 ][i]; } for (int i=1 ;i<=n;i++){ for (int j=2 ;j<=k;j++){ dp[i][j] = INT_MIN; for (int m=j-1 ;m<i;m++){ dp[i][j] = max (dp[i][j], dp[m][j-1 ]*a[m+1 ][i]); } } } cout << dp[n][k] <<endl; } int main () int n, k, num; cin >> n >> k >> num; solution (n, k, num); return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 import java.util.Scanner;public class DP313 { public static void main (String args[]) { int n, k, num; Scanner sc = new Scanner (System.in); n = sc.nextInt(); k = sc.nextInt(); num = sc.nextInt(); solution(n, k, num); } public static void solution (int n, int k, int num) { int [][] a = new int [n+1 ][n+1 ], dp = new int [n+1 ][k+1 ]; for (int i=1 ;i<=n;i++){ for (int j=i;j<=n;j++){ a[i][j] = Integer.parseInt(Integer.toString(num).substring(i-1 , j)); } } for (int i=1 ;i<=n;i++){ dp[i][1 ] = a[1 ][i]; } for (int i=1 ;i<=n;i++){ for (int j=2 ;j<=k;j++){ dp[i][j] = Integer.MIN_VALUE; for (int m=j-1 ;m<i;m++){ dp[i][j] = Math.max(dp[i][j], dp[m][j-1 ]*a[m+1 ][i]); } } } System.out.println(dp[n][k]); } }
测试输入与输出 输入:
3 2
312
输出:
62
314 最少费用购物问题 问题描述 商店中每种物品都有标价。例如,一朵花的价格是2元,一个花瓶的价格是5元,为了吸引顾客,商店提供了一组优惠商品价,优惠商品是把一种或多种商品分成一组,并降价销售,例如,3朵花的价格是5元,2个花瓶+1朵花的价格是10元,设计一个算法,计算出某顾客购买商品应付的最少费用。
输入格式 input.txt提供欲购物信息,第一行输入为B(0-5),此后的B行每行有三个数C K P,分别表示商品编号(1-999),购买总数(1-5),商品单价,一次最多购买5*5件商品。
offer.txt提供优惠商品价数据,文件中的第一行有一个整数S,表示有S种优惠组合,接下来的S行,每行的第一个数表示组合中的商品种类j,接下来是j个数字对(C K),C为商品编号,K为在优惠组合中的数量,最后一个数字P表示该组合的优惠价。输出最少费用。
算法设计 由于每次购买的商品最多五种,可以使用一个五维数组保存购买情况,用dp[i][j][k][l][p]表示购买的五种商品有i,j,k,l,p个时的最少费用。求最少费用时,遍历每种优惠组合,更新dp数组,设offer[m][c]表示第m个优惠组合中,商品c的数量,c取1-5,在读入时就只读入欲购买的商品。以下是考虑优惠组合时的递推方程,每种情况应该先初始化为用单价购买的价格,然后遍历组合找到最小值。
其中offer[m][0]表示优惠组合m的价格。
如果i-offer[m][i]<0,应该取0,这样就包含了凑单的情况。
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 #include <iostream> #include <fstream> #include <cmath> #include <climits> using namespace std;struct good { int id = -1 , n = 0 , p = 0 ; }; class solution {private : int B, C, K, S; int offer[101 ][6 ]; int dp[6 ][6 ][6 ][6 ][6 ]; good goods[6 ]; public : void input () void solve () }; int main () solution s; s.input (); s.solve (); return 0 ; } void solution::input () fstream in; in.open ("input314.txt" , ios::in); in >> B; for (int i=1 ;i<=B;i++){ in >> goods[i].id >> goods[i].n >> goods[i].p; } in.close (); for (int i=0 ;i<=101 ;i++){ for (int j=0 ;j<=6 ;j++) offer[i][j] = 0 ; } in.open ("offer.txt" , ios::in); in >> S; for (int i=1 ;i<=S;i++){ int t; in >> t; for (int j=0 ;j<t;j++){ in >> C >> K; for (int k=1 ;k<=B;k++){ if (goods[k].id==C){ offer[i][k] = K; break ; } } } in >> offer[i][0 ]; } in.close (); } void solution::solve () dp[0 ][0 ][0 ][0 ][0 ] = 0 ; for (int i=0 ;i<=goods[1 ].n;i++){ for (int j=0 ;j<=goods[2 ].n;j++){ for (int k=0 ;k<=goods[3 ].n;k++){ for (int l=0 ;l<=goods[4 ].n;l++){ for (int p=0 ;p<=goods[5 ].n;p++){ int minPrice = i*goods[1 ].p + j*goods[2 ].p + k*goods[3 ].p + l*goods[4 ].p + p*goods[5 ].p; dp[i][j][k][l][p] = minPrice; for (int m=1 ;m<=S;m++){ minPrice = min (minPrice, dp[max (0 , i-offer[m][1 ])][max (0 , j-offer[m][2 ])][max (0 , k-offer[m][3 ])][max (0 , l-offer[m][4 ])][max (0 , p-offer[m][5 ])]+offer[m][0 ]); } dp[i][j][k][l][p] = minPrice; } } } } } cout << dp[goods[1 ].n][goods[2 ].n][goods[3 ].n][goods[4 ].n][goods[5 ].n] << endl; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 import java.util.Scanner;import java.io.FileReader;public class DP314 { public static void main (String args[]) { solution s = new solution (); s.initialize(); s.input(); s.solve(); } } class good { int id, n, p; public good () {id=-1 ;n=0 ;p=0 ;} } class solution { private int B, C, K, S; private int [][] offer; private int [][][][][] dp; private good[] goods; public void initialize () { offer = new int [101 ][6 ]; dp = new int [6 ][6 ][6 ][6 ][6 ]; goods = new good [6 ]; for (int i=1 ;i<=5 ;i++) goods[i] = new good (); } public void input () { try (Scanner sc1 = new Scanner (new FileReader ("input314.txt" ))){ B = sc1.nextInt(); for (int i=1 ;i<=B;i++){ goods[i].id = sc1.nextInt(); goods[i].n = sc1.nextInt(); goods[i].p = sc1.nextInt(); } }catch (Exception e) { System.out.println(e.getClass()); } try (Scanner sc2 = new Scanner (new FileReader ("offer.txt" ))){ S = sc2.nextInt(); for (int i=1 ;i<=S;i++){ int t; t = sc2.nextInt(); for (int j=0 ;j<t;j++){ C = sc2.nextInt(); K = sc2.nextInt(); for (int k=1 ;k<=B;k++){ if (goods[k].id==C){ offer[i][k] = K; break ; } } } offer[i][0 ] = sc2.nextInt(); } }catch (Exception e) { System.out.println(e.getClass()); } } public void solve () { for (int i=0 ;i<=goods[1 ].n;i++){ for (int j=0 ;j<=goods[2 ].n;j++){ for (int k=0 ;k<=goods[3 ].n;k++){ for (int l=0 ;l<=goods[4 ].n;l++){ for (int p=0 ;p<=goods[5 ].n;p++){ int minPrice = i*goods[1 ].p + j*goods[2 ].p + k*goods[3 ].p + l*goods[4 ].p + p*goods[5 ].p; dp[i][j][k][l][p] = minPrice; for (int m=1 ;m<=S;m++){ minPrice = Math.min(minPrice, dp[Math.max(0 , i-offer[m][1 ])][Math.max(0 , j-offer[m][2 ])][Math.max(0 , k-offer[m][3 ])][Math.max(0 , l-offer[m][4 ])][Math.max(0 , p-offer[m][5 ])]+offer[m][0 ]); } dp[i][j][k][l][p] = minPrice; } } } } } System.out.println(dp[goods[1 ].n][goods[2 ].n][goods[3 ].n][goods[4 ].n][goods[5 ].n]); } }
测试输入与输出 测试1
输入:
input.txt
2
7 3 2
8 2 5
offer.txt
2
1 7 3 5
2 7 1 8 2 10
输出:
14
测试2
输入:
input.txt
5
offer.txt
6
输出:
2
315 收集样本问题 问题描述 机器人在一个nxn方格区域收集样本,(i,j)方格中的样本价值为v(i,j),机器人从左上角的第一个点出发,向右或向下移动到达右下角的点,在走过的路上收集样本,共走两次,设计一个算法,计算两次行走能够收集的样本最大价值。
输入格式 第一行的正整数n表示区域为nxn,接下来每行有三个整数x,y,v,表示(x,y)有价值为v的样本,直到输入为0 0 0结束。
算法设计 设dp[i][j]表示走到(i,j)能够收集的样本最大价值,则递推方程为:
记录走过的路径,将最优路径的值回溯清空,然后再次计算,得到两次行走的最大价值。
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <iostream> #include <cmath> #include <algorithm> using namespace std;const int maxn = 100 ;const int Up = 0 ;const int Left = 1 ;int v[maxn][maxn];int dp[maxn][maxn];int path[maxn][maxn];void clear (int x, int y) if (x<0 || y<0 ) return ; v[x][y] = 0 ; if (path[x][y]==Up){ clear (x-1 , y); } else clear (x, y-1 ); } int collect (int n) fill (dp[0 ], dp[0 ]+n*n, 0 ); for (int i=1 ;i<n;i++){ dp[i][0 ] = dp[i-1 ][0 ] + v[i][0 ]; path[i][0 ] = Up; dp[0 ][i] = dp[0 ][i-1 ] + v[0 ][i]; path[0 ][i] = Left; } for (int i=1 ;i<n;i++){ for (int j=1 ;j<n;j++){ dp[i][j] = max (dp[i-1 ][j], dp[i][j-1 ]) + v[i][j]; path[i][j] = (dp[i-1 ][j]>dp[i][j-1 ])?Up:Left; } } clear (n-1 , n-1 ); return dp[n-1 ][n-1 ]; } int main () int n, x, y, val, res; cin >> n; while (cin>>x>>y>>val){ if (x==0 && y==0 && val==0 ) break ; v[x-1 ][y-1 ] = val; } res = collect (n); res += collect (n); cout << res << endl; return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 import java.util.Scanner;import java.util.Arrays;class solution { private final int maxn = 100 ; private final int Up = 0 ; private final int Left = 1 ; private int n; private int [][] v; private int [][] dp; private int [][] path; public solution (int n) { this .n = n; v = new int [maxn][maxn]; dp = new int [maxn][maxn]; path = new int [maxn][maxn]; } public void addSample (int x, int y, int val) {v[x][y] = val;} public void clear (int x, int y) { if (x<0 || y<0 ) return ; v[x][y] = 0 ; if (path[x][y]==Up) clear(x-1 , y); else clear(x, y-1 ); } public int collect () { for (int i=0 ;i<n;i++) Arrays.fill(dp[i], 0 ); for (int i=1 ;i<n;i++){ dp[i][0 ] = dp[i-1 ][0 ] + v[i][0 ]; path[i][0 ] = Up; dp[0 ][i] = dp[0 ][i-1 ] + v[0 ][i]; path[0 ][i] = Left; } for (int i=1 ;i<n;i++){ for (int j=1 ;j<n;j++){ dp[i][j] = Math.max(dp[i-1 ][j], dp[i][j-1 ]) + v[i][j]; path[i][j] = (dp[i-1 ][j]>dp[i][j-1 ])?Up:Left; } } clear(n-1 , n-1 ); return dp[n-1 ][n-1 ]; } } public class DP315 { public static void main (String args[]) { int n, x, y, val, res; Scanner sc = new Scanner (System.in); n = sc.nextInt(); solution s = new solution (n); while (true ){ x = sc.nextInt(); y = sc.nextInt(); val = sc.nextInt(); if (x==0 && y==0 && val==0 ) break ; s.addSample(x-1 , y-1 , val); } res = s.collect(); res += s.collect(); System.out.println(res); } }
测试输入与输出 输入:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出:
67
316 最优时间表问题(线性DP) 传送门:https://www.luogu.com.cn/problem/P1280
问题描述 一台精密仪器的工作时间为n个时间单位。与仪器工作时间同步进行若干仪器维修程序。一旦启动维修程序,仪器必须进入维修。如果只有一个维修程序,必须进入该程序,如果在同一时刻有多个维修程序,可任选进入其中任何一个维修程序。维修程序必须从头开始,不得从中间插入,一个维修程序从第s个时间单位开始,持续t个时间单位,则该维修程序在第s+t-1个时间单位结束。为了提高仪器使用率,尽可能减少仪器维修的时间。
设计一个算法,对于给定的维修程序时间表,计算最短维修时间。
输入格式 第一行有两个正整数n和k,表示工作时间和维修程序数,接下来的k行每行有两个数s和t,表示维修程序的开始时间和持续时间。
算法设计 如果正向计算最短维修时间或最大工作时间,当前作出的选择会影响后续的选择,选择短还是长的维修程序与后续的程序有关。可以反向计算最大工作时间,用dp[i]表示i到n的最小维修时间,如果时刻i没有维修开始,dp[i] = dp[i+1],如果时刻i有维修开始,则dp[i] = min{dp[m[j].end_time]+m[j].t},m[j]表示从i时刻开始的维修。
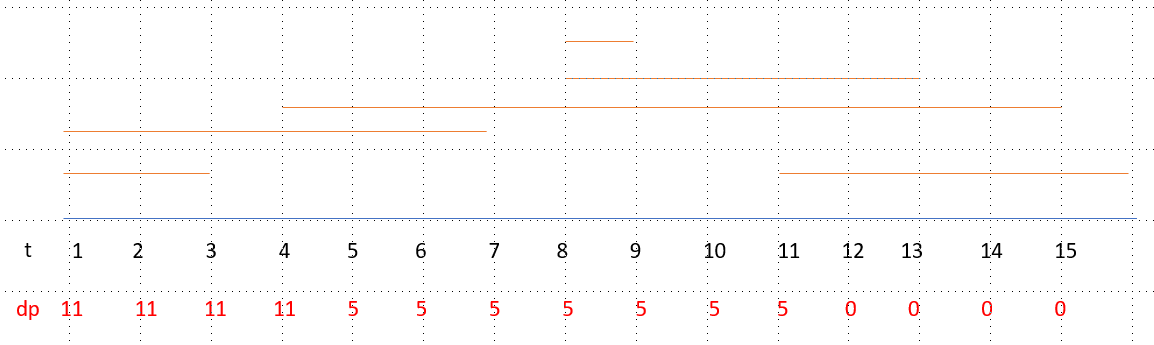
对于测试输入与输出,时间线和dp值如下:
当考虑i时刻到n时刻的最短维修时间时,只要m[i].end_time大于此后某一维修x的开始时间,计算的值就是没有进行维修x的i到n时刻的维修时间。
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <iostream> #include <cmath> #include <algorithm> using namespace std;struct maintenance { int s, t, end_time; bool operator < (const maintenance &a){ return s > a.s; } }; void solution (int n, int k, maintenance m[], int t[]) int dp[n+1 ], mi; mi = 0 ; sort (m, m+k); dp[n] = 0 ; for (int i=n-1 ;i>=1 ;i--){ if (t[i]==0 ) dp[i] = dp[i+1 ]; else { dp[i] = dp[m[mi].end_time] + m[mi++].t; for (int j=1 ;j<t[i];j++){ dp[i] = min (dp[i], dp[m[mi].end_time]+m[mi++].t); } } } cout << dp[1 ] <<endl; } int main () int n, k, s, t; cin >> n >> k; int T[n+1 ]; maintenance m[k]; fill (T, T+n+1 , 0 ); for (int i=0 ;i<k;i++){ cin >> s >> t; T[s]++; m[i].s = s; m[i].t = t; m[i].end_time = s + t - 1 ; } solution (n, k, m, T); return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 import java.util.Scanner;import java.util.Arrays;import java.util.Comparator;class maintenance { public int s, t, end_time; } public class DP316 { private static int n, k; public static void main (String args[]) { Scanner sc = new Scanner (System.in); n = sc.nextInt(); k = sc.nextInt(); maintenance[] m = new maintenance [k]; for (int i=0 ;i<k;i++) m[i] = new maintenance (); int s, t; int [] T = new int [n+1 ]; for (int i=0 ;i<k;i++){ s = sc.nextInt(); t = sc.nextInt(); T[s]++; m[i].s = s; m[i].t = t; m[i].end_time = s + t - 1 ; } solution(m, T); } public static void solution (maintenance[] m, int [] t) { int mi = 0 ; int [] dp = new int [n+1 ]; Arrays.sort(m, new Comparator <maintenance>(){ @Override public int compare (maintenance a, maintenance b) { return (a.s < b.s)?1 :(a.s == b.s)?0 :-1 ; } }); for (int i=n-1 ;i>=1 ;i--){ if (t[i]==0 ) dp[i] = dp[i+1 ]; else { dp[i] = dp[m[mi].end_time] + m[mi++].t; for (int j=1 ;j<t[i];j++){ dp[i] = Math.min(dp[i], dp[m[mi].end_time]+m[mi].t); mi++; } } } System.out.println(dp[1 ]); } }
测试输入与输出 输入:
15 6
1 2
1 6
4 11
8 5
8 1
11 5
输出:
11
317 字符串比较问题 问题描述 对于长度相同的两个字符串A和B,其距离定义为相应位置字符距离之和。两个非空格字符的距离是他们ASCII编码差的绝对值,空格与空格的距离为0,空格与其他字符的距离为一定值k。
一般情况下,A和B的长度不一定相同,A的扩展是在A中插入若干空格字符产生的字符串。在A和B所有长度相同的扩展中,有一对距离最小的扩展,该距离称为A和B的扩展距离。
设计一个算法,计算给定字符串A和B的扩展距离。
输入格式 前两行为字符串A和B,第三行为空格与其他字符的距离k。
算法设计 对于A的第i个字符Ai和B的第j个字符Bj,扩展情况下两个字符的匹配只有三种情况:
Ai与B的前j-1个字符匹配,Bj与空格匹配
Ai与空格匹配,Bj与A的前i-1个字符匹配
Ai与Bj匹配
用dp[i][j]来表示A的前i个字符和B的前j个字符的扩展距离,可根据以上三种情况写出递推方程:
代码实现 c++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <iostream> #include <cmath> #include <cstring> #include <algorithm> using namespace std;void solution (string a, string b, int k) int m, n; m = a.length (); n = b.length (); int dp[m+1 ][n+1 ]; fill (dp[0 ], dp[0 ]+(m+1 )*(n+1 ), 0 ); for (int i=0 ;i<=m;i++) dp[i][0 ] = i*k; for (int i=0 ;i<=n;i++) dp[0 ][i] = i*k; for (int i=1 ;i<=m;i++){ for (int j=1 ;j<=n;j++){ dp[i][j] = min (dp[i-1 ][j]+k, min (dp[i][j-1 ]+k, dp[i-1 ][j-1 ]+abs (a[i-1 ]-b[j-1 ]))); } } cout << dp[m][n] << endl; } int main () int k; string a, b; cin >> a >> b >> k; solution (a, b, k); return 0 ; }
java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 import java.util.Scanner;public class DP317 { public static void main (String args[]) { int k; String a, b; Scanner sc = new Scanner (System.in); a = sc.next(); b = sc.next(); k = sc.nextInt(); solution(a, b, k); } public static void solution (String a, String b, int k) { int m, n; m = a.length(); n = b.length(); int [][] dp = new int [m+1 ][n+1 ]; for (int i=0 ;i<=m;i++) dp[i][0 ] = i*k; for (int i=0 ;i<=n;i++) dp[0 ][i] = i*k; for (int i=1 ;i<=m;i++){ for (int j=1 ;j<=n;j++){ dp[i][j] = Math.min(dp[i-1 ][j]+k, Math.min(dp[i][j-1 ]+k, dp[i-1 ][j-1 ]+Math.abs(a.charAt(i-1 )-b.charAt(j-1 )))); } } System.out.println(dp[m][n]); } }
测试输入与输出 输入:
cmc
snmn
2
输出:
10