算法设计与分析-线性dp题目记录。
P1020 导弹拦截
题目描述
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度,计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入格式与输出格式
输入:
一行,若干个整数,中间由空格隔开。
输出:
两行,每行一个整数,第一个数字表示这套系统最多能拦截多少导弹,第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
样例输入与输出
输入:
1
| 389 207 155 300 299 170 158 65
|
输出:
提示
对于前 $50\%$ 数据(NOIP 原题数据),满足导弹的个数不超过 $10^4$ 个。该部分数据总分共 $100$ 分。可使用$\mathcal O(n^2)$ 做法通过。
对于后 $50\%$ 的数据,满足导弹的个数不超过 $10^5$ 个。该部分数据总分也为 $100$ 分。请使用 $\mathcal O(n\log n)$ 做法通过。
对于全部数据,满足导弹的高度为正整数,且不超过 $5\times 10^4$。
此外本题开启 spj,每点两问,按问给分。
算法设计
问题的本质是求最长不上升子序列的长度。
可以使用tail[i]表示长度为i的不上升子序列的尾元素,要求最长的不上升子序列,应该让尾元素尽量更大,子序列才可能更长。如果遇到一个大于最大长度的尾元素的元素,就用这个元素更新某个特定长度i的尾元素,这样长度i的单调递减序列就可能添加新的元素。如果遇到一个小于等于最大长度的尾元素的元素,那么可以将最大长度+1,将这个元素作为尾元素。
对于特定长度i的序列的尾元素的更新,可以使用二分搜索的方法,因为tail数组一定是一个递减的数组。
第二问使用贪心算法,使用已有系统中最后一枚导弹最低的系统进行拦截,如果不存在,使用一个新的系统。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String args[]) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
String line = bf.readLine();
String[] temp = line.split(" ");
int n = temp.length;
int[] h = new int[n];
for(int i=0;i<n;i++) {
h[i] = Integer.parseInt(temp[i]);
}
System.gc();
int[] tail = new int[n+1];
int maxLen = 0;
int[] sys = new int[n+1];
int used = 0;
for(int i=0;i<n;i++) {
if(h[i] > tail[maxLen]) {
tail[binarySearch(tail, 0, maxLen, h[i])] = h[i];
}
else {
tail[++maxLen] = h[i];
}
int sys_used = -1, sys_h = Integer.MAX_VALUE;
for(int j=0;j<used;j++) {
if(sys[j]>=h[i]) {
if(sys[j]<sys_h) {
sys_used = j;
sys_h = sys[j];
}
}
}
if(sys_used==-1) sys[used++] = h[i];
else sys[sys_used] = h[i];
}
System.out.println(maxLen+1);
System.out.println(used);
}
public static int binarySearch(int[] a ,int left, int right, int e) {
while(left < right) {
int mid = left + (right-left)/2;
if(a[mid]<e) {
right = mid;
}
else {
left = mid+1;
}
}
return left;
}
}
|
以上的结果只能200分,增加的sub-task数据TLE。对于第二问,根据Dilworth定理,需要的系统数是最长上升子序列的长度,修改为求最长上升子序列,就能优化通过最后的sub-task。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String args[]) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
String line = bf.readLine();
String[] temp = line.split(" ");
int n = temp.length;
int[] h = new int[n];
for(int i=0;i<n;i++) {
h[i] = Integer.parseInt(temp[i]);
}
System.gc();
int[] tail = new int[n+1];
int[] tail2 = new int[n+1];
int maxLen2, maxLen;
maxLen = maxLen2 = 1;
tail2[1] = tail[1] = h[0];
for(int i=1;i<n;i++) {
if(h[i] > tail[maxLen]) {
tail[binarySearch(tail, 1, maxLen, h[i])] = h[i];
}
else {
tail[++maxLen] = h[i];
}
if(h[i] <= tail2[maxLen2]) {
int x = binarySearch2(tail2, 1, maxLen2, h[i]);
if(x!=-1)
tail2[x] = h[i];
}
else {
tail2[++maxLen2] = h[i];
}
}
System.out.println(maxLen);
System.out.println(maxLen2);
}
public static int binarySearch(int[] a ,int left, int right, int e) {
while(left < right) {
int mid = left + (right-left)/2;
if(a[mid]<e) {
right = mid;
}
else {
left = mid+1;
}
}
return left;
}
public static int binarySearch2(int[] a ,int left, int right, int e) {
while(left < right) {
int mid = left + (right-left)/2;
if(a[mid]>e) {
right = mid;
}
else if(a[mid]==e) return -1;
else {
left = mid+1;
}
}
return left;
}
}
|
P1439 最长公共子序列
题目描述
给出 $1,2,\ldots,n$ 的两个排列 $P_1$ 和 $P_2$ ,求它们的最长公共子序列。
输入与输出格式
输入:
第一行是一个数 $n$。
接下来两行,每行为 $n$ 个数,为自然数 $1,2,\ldots,n$ 的一个排列。
输出:
一个数,即最长公共子序列的长度。
样例输入与输出
输入:
输出:
提示
- 对于 $50\%$ 的数据, $n \le 10^3$;
- 对于 $100\%$ 的数据, $n \le 10^5$。
算法设计
直接dp
用一般的动态规划方法,如果A[i]和B[I]相同,A和B的前i个元素的最长公共子序列长度为A和B前i-1元素的最长公共子序列的长度+1,如果不同,有两种可能:
- 长度为A前i-1元素和B的前i元素的最长公共子序列长度
- 长度为B前i-1元素和A的前i元素的最长公共子序列长度
最长子序列长度为这两种可能中的最大值。
用dp[i][j]表示A的前i项和B的前j项的最长公共子序列长度,按照以上的最优子结构填表就可以得到答案,但是时间复杂度是n^2,无法通过全部测试。
转化为最长上升子序列
该问题可以转化为一个最长上升子序列问题。可以将B中元素在A中的位置找出来,由于A和B都是1-n的一种排列,所以B中元素一定有在A中对应的位置,所有的位置形成一个新的序列,如果新序列存在子序列是上升的,则表示在B中子序列对应下标的元素在A中也是按顺序出现的,是公共子序列。这样最长公共子序列问题就转化为了最长上升子序列问题。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main{
public static void main(String args[]) throws IOException {
Reader r = new Reader();
int n = r.nextInt();
int[] a = new int[n+1];
int[] b = new int[n+1];
for(int i=1;i<=n;i++) a[i] = r.nextInt();
for(int i=1;i<=n;i++) b[i] = r.nextInt();
int[] map = new int[n+1];
for(int i=1;i<=n;i++) {
map[a[i]] = i;
}
int[] tail = new int[n+1];
int maxLen = 1;
tail[1] = map[b[1]];
for(int i=1;i<=n;i++) {
int temp = map[b[i]];
if(temp>tail[maxLen]) {
tail[++maxLen] = temp;
}
else {
int pos = binarySearch(tail, 1, maxLen, temp);
if(pos!=-1) tail[pos] = temp;
}
}
System.out.println(maxLen);
}
public static int binarySearch(int[] arr, int left, int right, int e) {
while(left<right) {
int mid = left + (right-left)/2;
if(arr[mid]==e) return -1;
else if(arr[mid]>e) {
right = mid;
}
else left = mid+1;
}
return left;
}
}
class Reader{
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public int nextInt() throws IOException {
st.nextToken();
return (int)st.nval;
}
}
|
P2758 编辑距离
题目描述
设 $A$ 和 $B$ 是两个字符串。我们要用最少的字符操作次数,将字符串 $A$ 转换为字符串 $B$。这里所说的字符操作共有三种:
- 删除一个字符;
- 插入一个字符;
- 将一个字符改为另一个字符。
$A, B$ 均只包含小写字母。
输入与输出格式
输入:
第一行为字符串 $A$;第二行为字符串 $B$;字符串 $A, B$ 的长度均小于 $2000$。
输出:
只有一个正整数,为最少字符操作次数。
样例输入与输出
输入:
输出
提示
对于 $100 \%$ 的数据,$1 \le |A|, |B| \le 2000$。
算法设计
用dp[i][j]表示A的前i项和B的前j项的匹配情况如果A[i-1]==B[i-1],则dp[i][j]=dp[i-1][j-1],不需要修改,如果A[i-1]!=B[j-1],则有三种修改方式,对应的修改次数为:
- 删除A[i]:dp[i-1][j]+1
- 向A中插入B[j]:dp[i][j-1]+1
- 将A[i]修改为B[j]:dp[i-1][j-1]+1
取以上三种的最小值。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main{
public static void main(String args[]) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
String a = bf.readLine();
String b = bf.readLine();
int lenA = a.length(), lenB = b.length();
int[][] dp = new int[lenA+1][lenB+1];
for(int i=0;i<=lenA;i++) dp[i][0] = i;
for(int j=0;j<=lenB;j++) dp[0][j] = j;
for(int i=1;i<=lenA;i++) {
for(int j=1;j<=lenB;j++) {
if(a.charAt(i-1)==(b.charAt(j-1))) dp[i][j] = dp[i-1][j-1];
else dp[i][j] = Math.min(dp[i-1][j], Math.min(dp[i][j-1], dp[i-1][j-1]))+1;
}
}
System.out.println(dp[lenA][lenB]);
}
}
|
P1040 加分二叉树
题目描述
设一个 $n$ 个节点的二叉树 $\text{tree}$ 的中序遍历为$(1,2,3,\ldots,n)$,其中数字 $1,2,3,\ldots,n$ 为节点编号。每个节点都有一个分数(均为正整数),记第 $i$ 个节点的分数为 $d_i$,$\text{tree}$ 及它的每个子树都有一个加分,任一棵子树 $\text{subtree}$(也包含 $\text{tree}$ 本身)的加分计算方法如下:
$\text{subtree}$ 的左子树的加分 $\times$ $\text{subtree}$ 的右子树的加分 $+$ $\text{subtree}$ 的根的分数。
若某个子树为空,规定其加分为 $1$,叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为 $(1,2,3,\ldots,n)$ 且加分最高的二叉树 $\text{tree}$。要求输出
$\text{tree}$ 的最高加分。
$\text{tree}$ 的前序遍历。
输入与输出格式
输入:
第 $1$ 行 $1$ 个整数 $n$,为节点个数。
第 $2$ 行 $n$ 个用空格隔开的整数,为每个节点的分数
输出:
第 $1$ 行 $1$ 个整数,为最高加分($ Ans \le 4,000,000,000$)。
第 $2$ 行 $n$ 个用空格隔开的整数,为该树的前序遍历。
样例输入与输出
输入:
输出:
提示
对于全部的测试点,保证 $1 \leq n< 30$,节点的分数是小于 $100$ 的正整数,答案不超过 $4 \times 10^9$。
算法设计
想不到加分是和区间子树取根决定,直接看题解了。
https://bubbleioa.blog.luogu.org/solution-p1040
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main{
private static int[][] root;
private static long[][] dp;
private static int[] score;
public static void main(String args[]) throws IOException {
Reader r = new Reader();
int n = r.nextInt();
score = new int[n+1];
for(int i=1;i<=n;i++) score[i] = r.nextInt();
dp = new long[n+1][n+1];
root = new int[n+1][n+1];
long result = _dp(1, n);
System.out.println(result);
pre_traverse(1, n);
}
public static long _dp(int i, int j) {
if(dp[i][j]!=0) return dp[i][j];
if(i==j) {
dp[i][i] = score[i];
root[i][i] = i;
return score[i];
}
dp[i][j] = _dp(i+1,j) + score[i];
root[i][j] = i;
for(int k=i+1;k<j;k++) {
long temp = _dp(i,k-1)*_dp(k+1,j)+score[k];
if(temp>dp[i][j]) {
dp[i][j] = temp;
root[i][j] = k;
}
}
return dp[i][j];
}
public static void pre_traverse(int i, int j) {
if(i>j) return;
System.out.print(root[i][j]+" ");
if(i<j) {
pre_traverse(i, root[i][j]-1);
pre_traverse(root[i][j]+1, j);
}
}
}
class Reader{
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public int nextInt() throws IOException {
st.nextToken();
return (int)st.nval;
}
}
|
P4933大师
题目描述
ljt12138 首先建了 $n$ 个特斯拉电磁塔,这些电塔排成一排,从左到右依次标号为 $1$ 到 $n$,第 $i$ 个电塔的高度为 $h[i]$。
建筑大师需要从中选出一些电塔,然后这些电塔就会缩到地下去。这时候,如果留在地上的电塔的高度,从左向右构成了一个等差数列,那么这个选择方案就会被认为是美观的。
建筑大师需要求出,一共有多少种美观的选择方案,答案模 $998244353$。
注意,如果地上只留了一个或者两个电塔,那么这种方案也是美观的。地上没有电塔的方案被认为是不美观的。
同时也要注意,等差数列的公差也可以为负数。
输入与输出格式
输入:
第一行一个正整数 $n$。
第二行 $n$ 个非负整数,第 $i$ 个整数是第 $i$ 个电塔的高度 $h[i]$。
输出:
输出一个整数,表示美观的方案数模 $998244353$ 的值。
样例输入与输出
输入:
1
2
| 8
13 14 6 20 27 34 34 41
|
输出:
输入:
1
2
| 100
90 1004 171 99 1835 108 81 117 141 126 135 144 81 153 193 81 962 162 1493 171 1780 864 297 180 532 1781 189 1059 198 333 1593 824 207 1877 216 270 225 1131 336 1875 362 234 81 288 1550 243 463 1755 252 406 261 270 279 288 1393 261 1263 297 135 333 872 234 881 180 198 81 225 306 180 90 315 81 81 198 252 81 297 1336 1140 1238 81 198 297 661 81 1372 469 1132 81 126 324 333 342 81 351 481 279 1770 1225 549
|
输出:
提示
设 $v$ 为最高的电塔高度。
对于前 $30\%$ 的数据,$n \le 20 $。
对于前 $60\%$ 的数据,$n \le 100$,$v \le 2 \times 10^3$。
对于另外 $20\%$ 的数据,所有电塔的高度构成一个等差数列。
对于 $100\%$ 的数据,$n \le 10^3$,$v \leq2 \times 10^4$。
算法设计
考虑线性dp,如果前面的元素的等差数列数已知,此后的元素应该可以借助前面的元素的等差数列数求解。如果前i-1项里面的元素可以形成一些公差为k的等差数列,那么只要第i项比这个等差数列中的任意一项大k,就可以接在该项后形成新的等差数列。例如前i-1项可以形成等差数列1;1 3;1 3 5;,新的元素只要是减去1 3 5等于公差2的元素,都可以形成一个公差为2的新序列(由于题目背景是建塔,两个相同的序列可以表示不同建塔情况)。因此,对于公差k,只要新的元素比之前所有公差k的数列的最后一项大k,就可以产生新序列。而k可以通过枚举找到所有可能的取值。
根据以上的分析,可以使用两维来表示状态,用dp[i][j]表示以第i项为最后一项,公差为j的长度大于1的数列数,递推式为:
其中,k枚举时只需要用h[i]-h[j]表示就可以了。公差存在负数情况,因此还要加一个偏置值(最大高度)。
最后考虑一下边界条件,只有一个塔或只有两个塔也是符合要求的,以上的递推式中,已经包含了只有两个塔的情况,没有一个塔的情况,最后只需要将结果加上n就可以了。
总数应该是dp[i][k]的矩阵和+n,可以直接在填表的过程中计算,每轮计算都加上dp[j][k]+1。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main{
private static int v;
private static int[] h;
private static int[][] dp;
private static final int mod = 998244353;
public static void main(String args[]) throws IOException {
Reader r = new Reader();
int n = r.nextInt();
h = new int[n+1];
for(int i=1;i<=n;i++) {
h[i] = r.nextInt();
v = Math.max(h[i], v);
}
dp = new int[n+1][2*v+1];
int result = 0;
for(int i=1;i<=n;i++) {
for(int j=1;j<i;j++) {
int k = h[i] - h[j] + v;
dp[i][k] = (dp[i][k] + dp[j][k] + 1) % mod;
result = (result + dp[j][k] + 1) % mod;
}
}
result = (result + n) % mod;
System.out.println(result);
}
}
class Reader{
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public int nextInt() throws IOException{
st.nextToken();
return (int)st.nval;
}
}
|
P1077 摆花
题目描述
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 $m$ 盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 $n$ 种花,从 $1$ 到 $n$ 标号。为了在门口展出更多种花,规定第 $i$ 种花不能超过 $a_i$ 盆,摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。
试编程计算,一共有多少种不同的摆花方案。
输入与输出格式
输入:
第一行包含两个正整数 $n$ 和 $m$,中间用一个空格隔开。
第二行有 $n$ 个整数,每两个整数之间用一个空格隔开,依次表示 $a_1,a_2, \cdots ,a_n$。
输出:
一个整数,表示有多少种方案。注意:因为方案数可能很多,请输出方案数对 $10^6+7$ 取模的结果。
样例输入与输出
输入:
输出:
提示
对于 $20\%$ 数据,有 $0<n \le 8,0<m \le 8,0 \le a_i \le 8$。
对于 $50\%$ 数据,有 $0<n \le 20,0<m \le 20,0 \le a_i \le 20$。
对于 $100\%$ 数据,有 $0<n \le 100,0<m \le 100,0 \le a_i \le 100$。
NOIP 2012 普及组 第三题
算法设计
摆花的顺序存在要求,标号大的必须排在后面,因此先摆标号小的,然后依据标号小的摆放方法数求标号大的摆放方法数。
设dp[i][j]表示前i-1种花,共摆j盆花的方法数,递推方程如下:
将前面i-1种花的摆放方式,用k盆花i替换掉最后的k盆花,就是新的摆放方式,dp[i][j]就是所有替换方式数的和。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main{
static int[] a;
static int[][] dp;
public static void main(String[] args) throws IOException {
Reader r = new Reader();
int n, m;
n = r.nextInt(); m = r.nextInt();
a = new int[n+1];
for(int i=1;i<=n;i++) {
a[i] = r.nextInt();
}
dp = new int[n+1][m+1];
dp[0][0] = 1;
for(int i=1;i<=n;i++) {
for(int j=0;j<=m;j++) {
for(int k=0;k<=a[i]&&k<=j;k++) {
dp[i][j] = (dp[i][j] + dp[i-1][j-k]) % 1000007;
}
}
}
System.out.println(dp[n][m]);
}
}
class Reader{
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public int nextInt() throws IOException {
st.nextToken();
return (int)st.nval;
}
}
|
P1233 木棍加工
题目描述
一堆木头棍子共有n根,每根棍子的长度和宽度都是已知的。棍子可以被一台机器一个接一个地加工。机器处理一根棍子之前需要准备时间。准备时间是这样定义的:
第一根棍子的准备时间为1分钟;
如果刚处理完长度为L,宽度为W的棍子,那么如果下一个棍子长度为Li,宽度为Wi,并且满足L>=Li,W>=Wi,这个棍子就不需要准备时间,否则需要1分钟的准备时间;
计算处理完n根棍子所需要的最短准备时间。比如,你有5根棍子,长度和宽度分别为(4, 9),(5, 2),(2, 1),(3, 5),(1, 4),最短准备时间为2(按(4, 9)、(3, 5)、(1, 4)、(5, 2)、(2, 1)的次序进行加工)。
输入与输出格式
输入:
第一行是一个整数n(n<=5000),第2行是2n个整数,分别是L1,W1,L2,w2,…,Ln,Wn。L和W的值均不超过10000,相邻两数之间用空格分开。
输出:
仅一行,一个整数,所需要的最短准备时间。
样例输入与输出
输入:
输出:
算法设计
长度和宽度是两维,不好进行计算,可以先对长度(或宽度)进行排序,这样就不用考虑长度,只需要按宽度来求最短准备时间。根据dilworth定理,最长不上升子序列的个数=最长上升子序列的长度,求宽度序列的最长上升子序列长度就是答案。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Comparator;
import java.util.Arrays;
public class Main{
static stick[] sticks;
static int[] tail;
public static void main(String[] args) throws IOException {
int n,l,w;
Reader r = new Reader();
n = r.nextInt();
sticks = new stick[n+1];
for(int i=1;i<=n;i++) {
l = r.nextInt();
w = r.nextInt();
sticks[i] = new stick(l,w);
}
Arrays.sort(sticks, 1, n+1 ,new Comparator<stick>() {
@Override
public int compare(stick a, stick b) {
if(a==null||b==null) return -1;
if(a.l<b.l) return 1;
if(a.l==b.l) {
if(a.w>b.w) return -1;
else return 1;
}
return -1;
}
});
tail = new int[n+1];
int maxLen = 1;
tail[1] = sticks[1].w;
for(int i=2;i<=n;i++) {
if(sticks[i].w>tail[maxLen]) {
tail[++maxLen] = sticks[i].w;
}
else {
int pos = Arrays.binarySearch(tail, 1, maxLen+1, sticks[i].w);
if(pos>0) continue;
else tail[-pos-1] = sticks[i].w;
}
}
System.out.println(+maxLen);
}
}
class stick{
public int l,w;
public stick(int l, int w) {
this.l = l;
this.w = w;
}
}
class Reader{
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public int nextInt() throws IOException {
st.nextToken();
return (int)st.nval;
}
}
|
这个题最大的收获是用了Arrays的排序和二分查找,尤其是排序,先对长度降序,相等时则按宽度降序,排序时发现一组数据无法通过:
3
1 1 1 2 1 3
原因是排序时按宽度降序没有排序成功,输出Comparator的参数a和b的地址,和原来stick数组的元素地址对应,发现a排在b的后面,又经过修改返回值发现,返回-1才是交换a和b,这和许多网上的解释是不一样的。
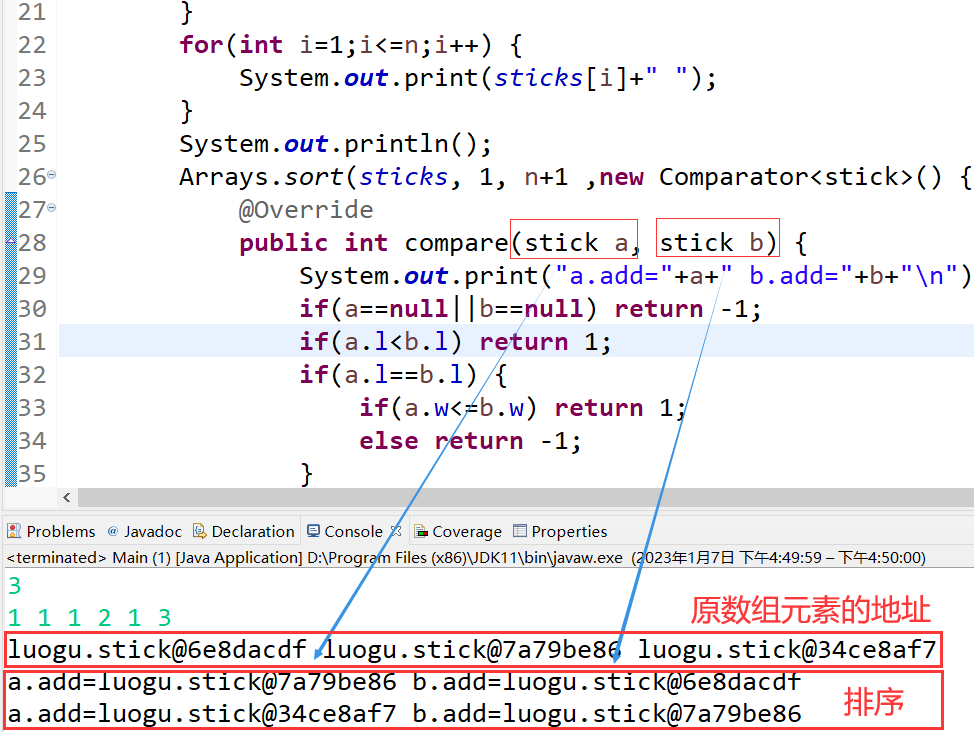
另外binarySearch如果没找到元素,假设插入位置下标为idx,返回值是-idx-1,这是为了修正0,避免返回0分不清是否找到元素。
P1091 合唱队形
题目描述
$n$ 位同学站成一排,音乐老师要请其中的 $n-k$ 位同学出列,使得剩下的 $k$ 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 $k$ 位同学从左到右依次编号为 $1,2,$ … $,k$,他们的身高分别为 $t_1,t_2,$ … $,t_k$,则他们的身高满足 $t_1< \cdots t_{i+1}>$ … $>t_k(1\le i\le k)$。
你的任务是,已知所有 $n$ 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
输入与输出格式
输入:
共二行。
第一行是一个整数 $n$($2\le n\le100$),表示同学的总数。
第二行有 $n$ 个整数,用空格分隔,第 $i$ 个整数 $t_i$($130\le t_i\le230$)是第 $i$ 位同学的身高(厘米)。
输出:
一个整数,最少需要几位同学出列。
样例输入与输出
输入:
1
2
| 8
186 186 150 200 160 130 197 220
|
输出:
提示
对于 $50\%$ 的数据,保证有 $n \le 20$。
对于全部的数据,保证有 $n \le 100$。
算法设计
合唱队形的人数取决于C位同学,队形中C位左侧的同学是C左侧所有同学身高形成的序列的最长上升子序列长度,同理,右侧最多的人数是最长下降子序列长度。所以只要求出以每个位置结束的序列的最长上升子序列长度,以每个位置开始的序列的最长下降子序列长度,然后枚举所有C位的最大人数就可以了。由于n<=100,计算最长上升子序列可以只用O(n^2)的方法,不用优化。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Comparator;
import java.util.Arrays;
public class Main{
static int[] h;
static int[] dp1;
static int[] dp2;
public static void main(String[] args) throws IOException {
int n;
Reader r = new Reader();
n = r.nextInt();
h = new int[n+1];
dp1 = new int[n+1];
dp2 = new int[n+1];
for(int i=1;i<=n;i++) {
h[i] = r.nextInt();
}
for(int i=1;i<=n;i++) {
dp1[i] = 1;
for(int j=1;j<i;j++) {
if(h[i]>h[j]) {
dp1[i] = Math.max(dp1[i], dp1[j]+1);
}
}
}
for(int i=n;i>=1;i--) {
dp2[i] = 1;
for(int j=i+1;j<=n;j++) {
if(h[i]>h[j]) {
dp2[i] = Math.max(dp2[i], dp2[j]+1);
}
}
}
int maxNum = 0;
for(int i=1;i<=n;i++) {
maxNum = Math.max(maxNum, dp1[i]+dp2[i]-1);
}
System.out.println(n-maxNum);
}
}
class Reader{
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public int nextInt() throws IOException {
st.nextToken();
return (int)st.nval;
}
}
|
P5858 「SWTR-03」Golden Sword
题目背景
小 E 不幸在一场战斗中失去了他的金宝剑。
题目描述
制造一把金宝剑需要 $n$ 种原料,编号为 $1$ 到 $n$,编号为 $i$ 的原料的坚固值为 $a_i$。
炼金是很讲究放入原料的顺序的,因此小 E 必须按照 $1$ 到 $n$ 的顺序依次将这些原料放入炼金锅。
但是,炼金锅的容量非常有限,它最多只能容纳 $w$ 个原料。
所幸的是,每放入一个原料之前,小 E 可以从中取出一些原料,数量不能超过 $s$ 个。
- 我们定义第 $i$ 种原料的耐久度为:放入第 $i$ 种原料时锅内的原料总数(包括正在放入的原料) $\times\ a_i$,则宝剑的耐久度为所有原料的耐久度之和。
小 E 当然想让他的宝剑的耐久度尽可能得大,这样他就可以带着它进行更多的战斗,请求出耐久度的最大值。
注:这里的“放入第 $i$ 种原料时锅内的原料总数包括正在放入锅中的原料,详细信息请见样例。
输入与输出格式
输入:
第一行,三个整数 $n,w,s$。
第二行,$n$ 个整数 $a_1,a_2,\dots,a_n$。
输出:
一行一个整数,表示耐久度的最大值。
样例输入与输出
输入:
输出:
输入:
输出:
输入:
输出:
输入:
输出:
提示
「样例说明」
- 对于样例 1,一种可行的最优方案为:
首先放进原料 1,此时锅内有 $1$ 种原料,耐久度为 $1\times a_1=1\times 1=1$。
再放进原料 2,此时锅内有 $2$ 种原料,耐久度为 $2\times a_2=2\times 3=6$。
再放进原料 3,此时锅内有 $3$ 种原料,耐久度为 $3\times a_3=3\times 2=6$。
取出原料 1,再放进原料 4,此时锅内有 $3$ 种原料,耐久度为 $3\times a_4=3\times 4=12$。
取出原料 4,再放进原料 5,此时锅内有 $3$ 种原料,耐久度为 $3\times a_5=3\times 5=15$。
最终答案为 $1+6+6+12+15=40$。
- 对于样例 2,一种可行的最优方案为:
放进原料 1,耐久度为 $1\times 1=1$。
取出原料 1,放进原料 2,耐久度为 $1\times (-3)=-3$。
放进原料 3,耐久度为 $2\times (-2)=-4$。
放进原料 4,耐久度为 $3\times 4=12$。
取出原料 2,放进原料 5,耐久度为 $3\times 5=15$。
最终答案为 $1+(-3)+(-4)+12+15=21$。
- 对于样例 3,一种可行的最优方案为:
$a_1+2a_2+2a_3+3a_4+4a_5+3a_6+4a_7=17$。
- 对于样例 4,一种可行的最优方案为:
$a_1+a_2+a_3+a_4+a_5=-15$。
「数据范围与约定」
- Subtask #1(15 points):$n\leq 10$。
- Subtask #2(5 points):$n\leq 100$,$a_i\geq0$。
- Subtask #3(15 points):$n\leq 300$。
- Subtask #4(15 points):$s=w=n$。
- Subtask #5(5 points):$a_i\geq 0$。
- Subtask #6(10 points):$n\leq 2\times 10^3$。
- Subtask #7(10 points):$s=1$。
- Subtask #8(25 points):无特殊限制。
对于 $100\%$ 的数据,$1 \leq s \leq w \leq n \leq 5\times 10^3$,$|a_i| \leq 10^9$。对于 Subtask $i$ 有 $|a_i|\leq 10^{i+1}$。
算法设计
放入一个原料和之前放入的原料有关,因此状态需要保存原料标号,放入原料时的原料耐久度与已放入的原料数有关,因此还需要保存原料数信息,因此可以用二维数组表示状态。设dp[i][j]表示前i种原料,共放入j种原料的耐久度,可写出递推方程:
其中k的取值范围是j-1到j+s-1,前i种原料有j-1种加入,可直接放入i;有j种加入,可以取出1种再放入i;有更多种加入,可以先取出到只剩j-1种,然后加入原料i,最多可以取出s种,因此k最大取j+s-1。
计算dp[i][j]时,对于不同的j值,可以发现k的区间每次都+1,然后从这个区间找最大值,这个过程中有重复的比较,可以使用单调队列进行优化。只要在求j值的时候建一个单调队列就可以了,第一维没有影响。并且dp[i][j]只需要用上一层的值,最后的结果也只需要dp[n][j]的最大值,因此可以使用滚动数组。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Comparator;
import java.util.Arrays;
public class Main{
private static long[] a;
private static long[][] dp;
private static int[] queue;
private static int head, tail;
public static void main(String[] args) throws IOException {
int n, w, s;
Reader r = new Reader();
n = r.nextInt(); w = r.nextInt(); s = r.nextInt();
a = new long[n+1];
dp = new long[2][w+1];
queue = new int[2*w+1];
for(int i=1;i<=n;i++) a[i] = r.nextInt();
Arrays.fill(dp[0], Long.MIN_VALUE/2);
Arrays.fill(dp[1], Long.MIN_VALUE/2);
int l = 0;
dp[0][0] = 0;
for(int i=1;i<=n;i++) {
l = l^1;
int head, tail;
head = tail = 0;
for(int j=Math.min(w,i); j>=1; j--) {
while(queue[head+1]>s+j-1&&head!=tail) head++;
while(dp[l^1][queue[tail]]<dp[l^1][j]&&head!=tail) tail--;
queue[++tail]=j;
dp[l][j]=Math.max(dp[l^1][queue[head+1]],dp[l^1][j-1]);
dp[l][j]+=j*a[i];
}
}
long result = Long.MIN_VALUE;
for(int i=1;i<=w;i++) {
result = Math.max(result, dp[l][i]);
}
System.out.println(result);
}
}
class Reader{
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public int nextInt() throws IOException {
st.nextToken();
return (int)st.nval;
}
}
|


