快速傅里叶变换是离散傅里叶变换（DFT）的快速算法。若x(n)是一个长度为M的有限长序列，则x(n)的N点DFT如下，式中$W_N=e^{-j\frac{2\pi}{N}}$。其计算可表示为矩阵乘向量$X=Fx$。

$W_N^{nk}$会均匀的分布复平面的单位圆上，具有一定的周期性。

  • $b = rN + a$，则$ W_N^{rN} = e^{-j2\pi r} = 1$，$
    W_N^{b} = W_N^{rN} \cdot W_N^{a} = W_N^{a} $
  • $b=ra$，且N可被r整除，则$WN^b=e^{-jra\frac{2\pi}{N}}=e^{-ja\frac{2\pi r}{N}}=W^a{\frac{N}{r}}$
  • $b=\frac{N}{2}+rN+a$，N为偶数，则$W_N^{b}=-W_N^a$

Radix-2 FFT

DFT算法的时间复杂度为$O(n^2)$，而Cooley Tuky算法将时间复杂度降低到$O(nlogn)$，本节讨论的是基为2的Cooley Tuky快速傅里叶变换。radix-2 FFT又分时域抽取(DIT-FFT)和频域抽取(DIF-FFT)。

1 DIT-FFT(时域抽取)

设$N=2^m$，可以将序列x(n)按照奇偶分为两个$\frac{N}{2}$的子序列。可以将其拆解为：

原序列的DFT可表示为：

根据周期性的第二条，可将两项转为：

$X_1(k)和X_2(k)$分别为两个子序列的$\frac{N}{2}$FFT，而由于周期性第三条，可以表示$X(k)$为：

所以奇偶序列中对应位置的值会通过以上两式产生相应的两个值，即蝶形运算：

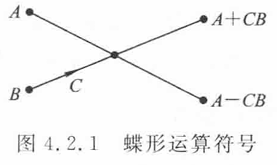
image-20250228185103823

对于一个8点DFT，时域分解由两组$\frac{N}{2}$DFT合并完成：

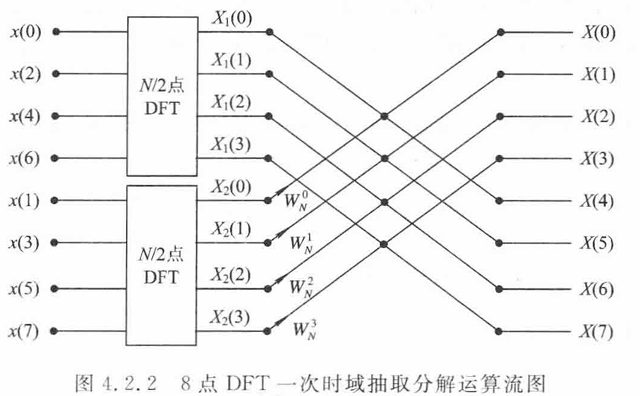
image-20250228185202485

构建$X_1$和$X_2$可以递归进行分解，从而得到二次时域分解抽取运算：

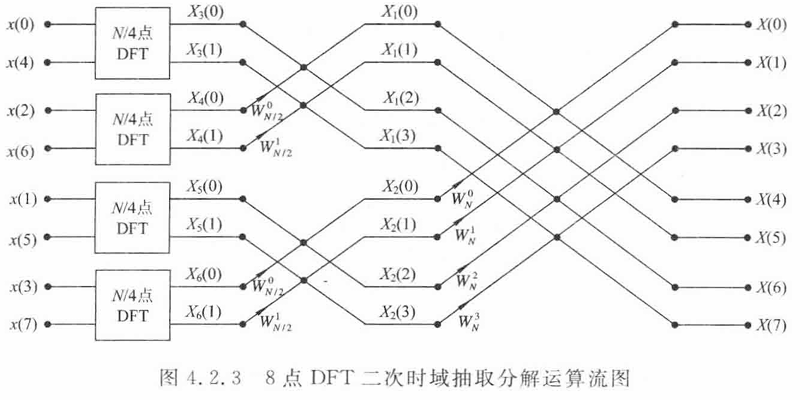
image-20250228185926242

只要N是2的幂次，就可以递归分解，直到单个值的DFT就是其本身，对于上述8点DFT，最后的分解结果运算图为：

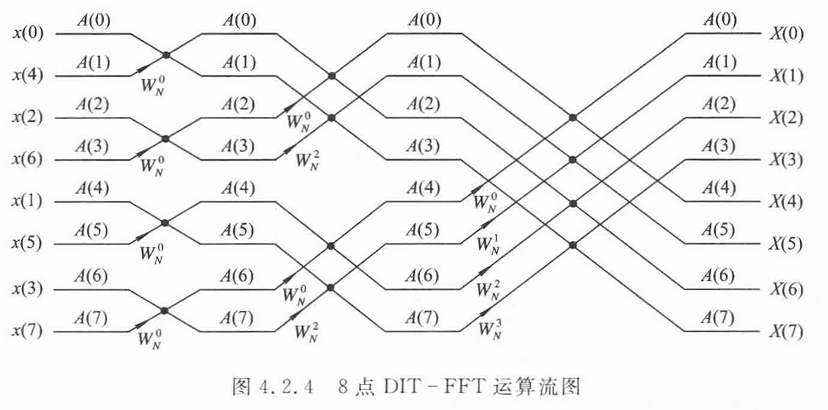
image-20250228190124489

图中的输入不是顺序排列，但是是有规律的，后续会继续讨论。还可以注意到$W^k_{\frac{N}{m}}$利用了周期性2变换为了$W^{mk}_N$。图中的数组A用于存放输入序列和每级运算结果，后续的编程方法的讨论会用到。

2 DIT-FFT的运算规律及编程思想

1.原位计算

由图4.2.4，$N=2^M$点的FFT进行M次运算，每级运算为$\frac{N}2$个蝶形运算，同一级的输入只对本次蝶形运算有用，而且每个蝶形的输入输出在同一条线上，因此计算完一个蝶形后，可以直接将输出数据存储到输入位置，进行原位计算，节省内存空间。

2.旋转因子的规律

蝶形计算需要乘旋转因子$W_N^p$，对于图4.2.4，从左到右用L表示运算级数且从1开始，则$N=2^L$，$p$是从0开始的序列，且长度为$2^{L-1}$，

因为

所以

这就是图4.2.4对于$W^k_{\frac{N}{m}}$变换的数学描述。

3.蝶形运算规律

对于图4.2.4一个蝶形运算轮次的前后，一个A由上一级的两个A运算得到，假设B表示两个输入数据之间的距离，则蝶形运算可表示为：

式中：

第L级中，每个鲽形的两个输入距离$B=2^{L-1}$个点，每级刚好也是有B个旋转因子，每个旋转因子对应间隔为$2^L$个点的$2^{M-L}$个蝶形。

4.运算

根据上述的运算规律，可以从输入的第一级开始，逐级完成计算，共进行M级运算。每次求出B个不同的旋转因子，并计算完他对应的$2^{M-L}$个蝶形。所以最终的程序包含三个循环，最外层为输入层级，第二层为旋转因子，共B个(记为迭代J)，第三层为旋转因子对应的不同蝶形(记为迭代k)，共$2^{M-L}$个，间隔为$2^L$，对应$A(J2^{kL})$和$A(J2^{kL}+B)$。

剩下的唯一问题就是将输入序列x(n)进行排序，使他们的排序符合奇偶抽取。

5.倒序

由于$N=2^M$，所以输入序列的顺序数可以用M位二进制表示，抽取相当于从最低位起每次取一位按照奇偶分组，该分组可以找出规律发现其二进制表示相当于顺序数的二进制位倒序，即位置在001的是x(100)的值。而生成倒序数数列的过程，为了方便表示，可以用J表示当前倒序数的十进制数值，对于$N=2^M$，最高位的十进制权值为N/2，向右的每位权值依次除2，所以按照顺序，每次下一个数都是当前倒序数最高位+1，相当于十进制运算J+N/2，如果最高位是0则得到下一个数，如果是1则要转为0(J-N/2)，向次高位进位，相当于J+N/4，依次类推，直到无进位，就得到了下一个倒序数。

得到了倒序数后，将原数组中的输入序列重新排列，由于第一个序列值和最后一个序列值不需要重排(000 111)，所以从A(I=1)开始，到A(N-2)，倒序数初值为N/2，计算出一个倒序数J时，就与默认顺序I比较，I=J时不需要交换，I不等于J时，A(I)和A(J)交换，避免重复调换，只对I<J的情况调换。

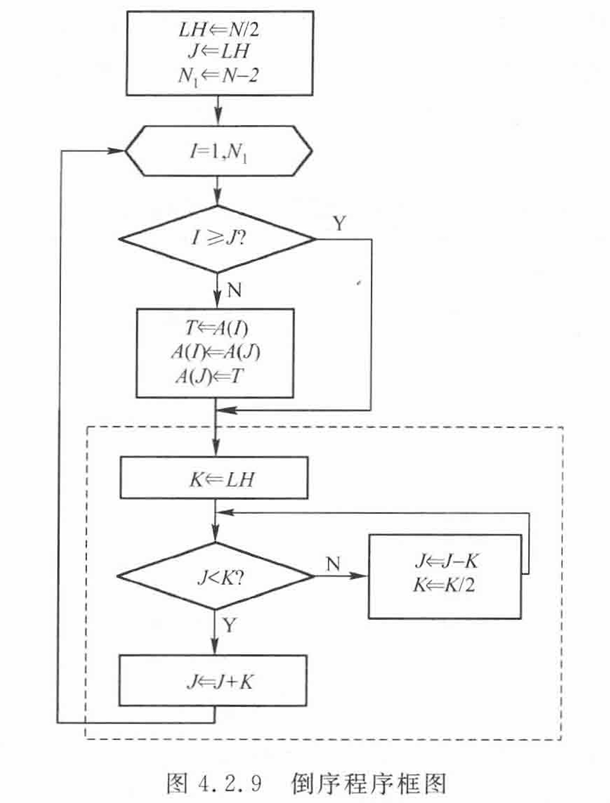
image-20250303115159714

6.实现

以下是对上述算法的一个实现，与上述程序框图完全一致。使用FFTW提供的复数类型，并对相同的输入数据计算检验了正确性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<fftw3.h>
#include<math.h>

void compute_twiddle_factor(int p, int N, fftw_complex &W) {
    double theta = 2.0 * M_PI * p / N;  // 计算角度
    W[0] = std::cos(theta);              
    W[1] = -std::sin(theta);              
}

void complex_multiply(const fftw_complex& a, const fftw_complex& b, fftw_complex& result) {
    result[0] = a[0] * b[0] - a[1] * b[1];  
    result[1] = a[0] * b[1] + a[1] * b[0];  
}

void complex_add(const fftw_complex& a, const fftw_complex& b, fftw_complex& result) {
    result[0] = a[0] + b[0];  
    result[1] = a[1] + b[1];  
}

void complex_subtract(const fftw_complex& a, const fftw_complex& b, fftw_complex& result) {
    result[0] = a[0] - b[0];  
    result[1] = a[1] - b[1];  
}

inline void reverse(fftw_complex *x, int N){
  int LH = N/2;
  int j = LH;
  int N1 = N-2;
  for(int i=1;i<=N-2;i++){
    if(i<j){
      double tmp_re = x[i][0];
      double tmp_im = x[i][1];
      x[i][0] = x[j][0];
      x[i][1] = x[j][1];
      x[j][0] = tmp_re;
      x[j][1] = tmp_im;
    }
    int k = LH;
    while(j>=k){
      j = j-k;
      k = k/2;
    }
    j = j+k;
  }
}

inline void fftKernel(fftw_complex *x, int N){
  int M = std::log2(N);
  for(int L=1;L<=M;L++){
    int B = (int)std::pow(2, L-1);
    for(int J=0;J<B;J++){
      int p = J*(1<<(M-L));
      fftw_complex Wnp;
      compute_twiddle_factor(p, N, Wnp);
      for(int K=J;K<N;K+=(int)std::pow(2,L)){
        fftw_complex WB;
        complex_multiply(x[K+B], Wnp, WB);
        fftw_complex out1;
        complex_add(x[K], WB, out1);      // 计算 A + WB
        complex_subtract(x[K], WB, x[K+B]); // 计算 A - WB
        x[K][0] = out1[0];
        x[K][1] = out1[1];
        //x[K+B][0] = out2[0];
        //x[K+B][1] = out2[1];
      }
    }
  }
}

void myFFT(fftw_complex* x, int N){
  reverse(x, N);
  fftKernel(x, N);
}

由于这是一个简单实现，性能差距与FFTW库的差别很大，计算8192*16的1D FFT，FFTW仅需要2ms，而上面这个实现需要25ms。

3 DIF-FFT(频域抽取)

频域抽取DIF-FFT是另一种常用的快速算法，这种算法中，同样将原序列分为两个子序列，但直接前后分开：

其中：

根据k取奇数或偶数，可以设：

其中 $n = 0, 1, 2, \ldots, \frac{N}{2} - 1$。可得：

偶数部分的X值是x1序列的N/2点DFT，奇数部分的值是x2序列的N/2点DFT，而x1和x2序列的值来源于蝶形计算：

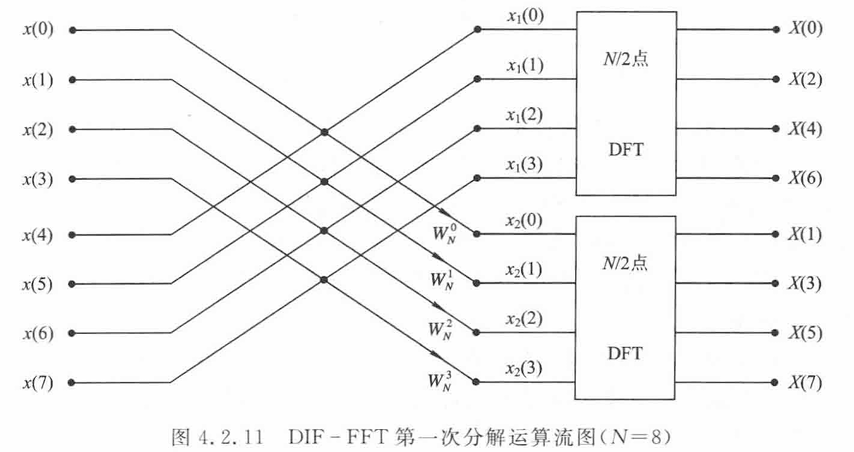
image-20250318153733625

而N/2的FFT可以用同样的方式分解为蝶形运算，直到最后的两点DFT：

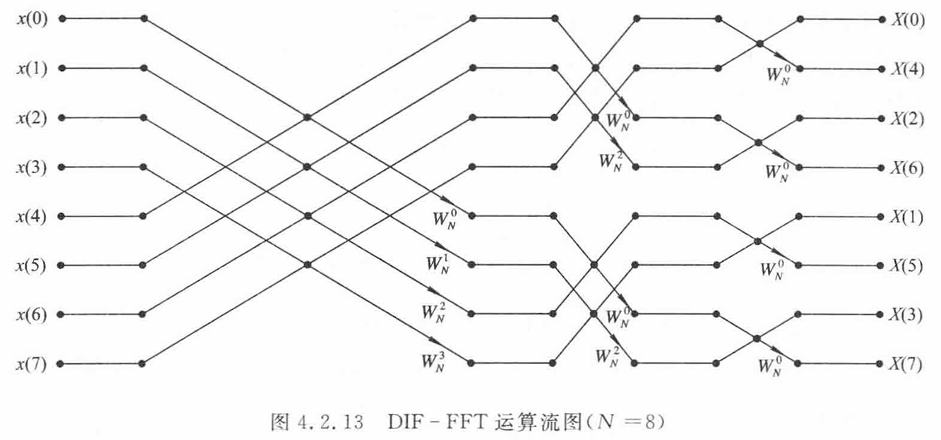
image-20250318154040000

DIF-FFT算法和DIT-FFT算法类似，运算次数也相同，但是DIF-FFT算法输出为倒序排列，需要对输出进行重新排序。蝶形运算上也稍有不同，DIT-FFT先乘后加减(A+CB、A-CB)，DIT-FFT则是先加减后相乘。

Radix-4 FFT

不同基数的FFT算法的运算效率不同，实际中最常用的是基2FFT、基4FFT，分裂基FFT和DHT。在基rFFT中，基4FFT算法效率与基8FFT很接近，但是实现更简单，判断开销少。

1 DIT-FFT

与基2FFT类似，首先将输入序列进行划分，抽取分为四份：

则x(n)的DFT可以表示为：

其中的$X_1(k)、X_2(k)$等分别为抽取为四份的四个序列的$\frac N4$点DFT，上面的公式只能计算$0$~$ \frac n4-1$的DFT，可以令$k=k+\frac N4$~$k+\frac{3N}{4}$，以及$W^{\frac N 4}=-j$的特性的得到完整的DFT结果序列：

$W^{\frac N 4}=-j$在复平面的图示，图中为radix=8的旋转因子[1]。

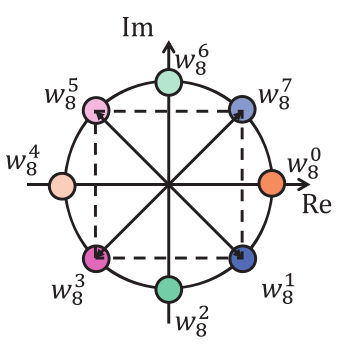
image-20250325154357066

1. 图源自OpenFFT-SME: An Efficient Outer Product Pattern FFT Library on ARM SME CPUs ↩

可以用矩阵形式表示四部分结果：

对第二个矩阵进行周期性变换：

对右边的向量展开到$\frac N4$列，并分解为逐元素乘：

因此基4FFT矩阵形式表达为：

而$X_{1、2、3、4}(k)$是$\frac N4$点DFT，可将矩阵形式表示记为：

这里已经可以看出，Cooley Tukey算法将序列转换为了2维，行内进行DFT，再从列的维度上进行DFT，即其计算本质仍然是DFT，只是通过重用减少了计算量。由于上述计算的数据是不连续的，所以可以预先通过转置调整其为连续数据，自底向上进行计算和合并的过程，最后一个参考链接给出了转置调整顺序的过程以及一个简单易懂的例子。

参考链接

1.数字信号系统

2.https://zhuanlan.zhihu.com/p/129420167

3.https://www.woaitingting.site/index.php/archives/10/