ScalapackTest
近期的工作需要熟悉scalapack的数据格式,做个简单记录。
采用了直接通过apt安装的方式:
1 | sudo apt-get install libscalapack-openmpi-dev |
如果是编译安装,可以指定:
1 | cmake -DCMAKE_INSTALL_PREFIX=/local \ |
简单编写的测试程序的cmake,注意到直接链接`$SCALAPACK_LIBRARIES会失败。这个包的.cmake没配置这个变量,也没有头文件和相应的头文件路径变量,链接的时候直接链接scalapack-openmpi就可以了。
1 | cmake_minimum_required(VERSION 3.12) |
简单的测试程序主要是为了理解scalapack的数据规格,调用简单选择了矩阵乘,其接口如下:1
2
3
4
5
6extern void pdgemm_(
char *transa, char *transb, int *m, int *n, int *k,
double *alpha, double *a, int *ia, int *ja, int *desca,
double *b, int *ib, int *jb, int *descb,
double *beta, double *c, int *ic, int *jc, int *descc
);
由于scalapack底层是fortran实现,所以首先要注意数据的起始索引是1。scalapack中,是否转置等是以char的方式传入,用N表示转置,T表示转置,C表示共轭转置。ia,ja等变量表示的是子矩阵在全局矩阵中的起始行列索引,索引从1开始。desc是数组,指向包含矩阵全局分布信息的描述符。
进程网格与矩阵描述符
scalapack通过内部的BLACS来管理进程网格和通信。通常情况下进入程序需要创建一个BLACS进程通信上下文,使用以下接口来创建:
1 | extern void Cblacs_get(int *context, int *scope, int *ictxt); |
第一个参数表示初始上下文标识符,-1表示创建新的上下文。第二个参数表示关联通信域,0表示默认的MPI_COMM_WORLD,最后一个参数用于返回新创建的上下文句柄。
创建上下文后,用以下接口创建进程网格,第二个参数用于控制进程分布的顺序,可以取Row和Col。
1 | extern void Cblacs_gridinit(int *ictxt, char *order, int nprow, int npcol); |
Cblacs_gridinfo接口用来获取当前进程在进程网格中的信息:
1 | extern void Cblacs_gridinfo( |
上述三个接口可以创建和获取进程网格的信息,接下来就要设置矩阵的划分信息了,首先获取本地维度:
1 | extern int numroc_( |
有了本地维度之后,需要初始化矩阵描述符:
1 | extern void descinit_( |
之后就可以用矩阵描述符传入计算接口来完成分布式计算了,scalapack的设计中,矩阵描述符和网格等信息和矩阵本身的存储都是分离的,所以要独立分配local_row*local_col的空间作为本地的矩阵数据存储空间,传入计算函数,需要注意大小和创建网格以及创建描述符时一致,并注意资源释放,要分别释放矩阵数据和进程网格,进程网格通过下面的接口释放:
1 | Cblacs_gridexit(int *ictxt); |
矩阵乘接口调用
以下是利用上面所述接口创建矩阵并调用scalapack矩阵乘的程序:
1 |
|
2D循环块存储
scalapack存储矩阵的方式是2D块循环,前面的测试代码只是简单了解下scalapack怎么使用,并没有体现数据的存储,因为数据都是直接随机生成的。接下来用一个测试程序看看2D块循环。
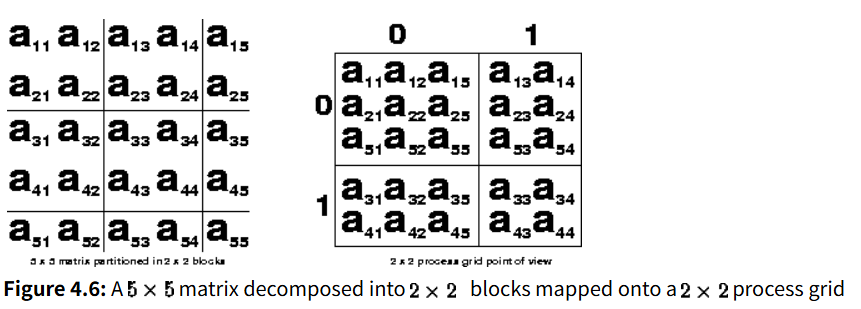
首先可以通过文档中的例子理解2D块循环的存储方式,下图是一个5x5矩阵划分为2x2矩阵块并存放到2x2进程网格上的示意。每个进程持有的行/列起始索引的差值都是BLOCKSIZE*nprocs,所有的自己负责的块统一按照列有限的顺序存储,这里需要注意的是本地存储不是按照块存储的,而是按照列来存储的,例如图中的划分后的矩阵,0号进程所持有的数据是顺序的a11 a21 a51 a12 a22 a52 a15 a25 a55,而不是按照划分的2x2块存储。
scalapack提供了一个矩阵重分发函数,我们使用这个函数来测试2D块循环:
1 | extern void pdgemr2d_( |
这个函数会把原矩阵描述符描述的矩阵分发到新的描述符中的各个进程。所以可以先在单进程上准备一个完整的矩阵,然后进行分发,检查各个进程上获取的2D块循环的数据是否和上面的描述是一致的。
1 |
|
输出如下,红框标出了进程0持有的块,下面按照顺序输出了进程0的矩阵存储,显然是先将所有数据拼到一块,然后再按列存储,而不是按块存储。

这种2D块存储的方式是为了将块划分的足够小,这样对于对角矩阵等局部稠密的矩阵能够尽可能每个进程的负载均衡。要将其转为一般的稀疏矩阵格式也可以通过上述的分发接口实现,首先固定块的大小让每个进程只持有一个块的数据,然后再重分发,在进程内部调整为稀疏格式。但是对于不对齐或者无法均分的情况,还要额外做个填充。



