偶然看到本科时体系结构课程老师实验室的一篇工作，是GPU上的SpMV，在suitsparse所有矩阵上性能表现优异，发表在TPDS24上，印象深刻，最近有时间阅读，做个仔细的笔记。

FastLoad: Speeding Up Data Loading of Both Sparse Matrix and Vector for SpMV on GPUs

1 概况

本篇工作是针对GPU CUDACORE计算SpMV的高性能实现，优化角度主要是负载均衡和加速访存。在整个suitSparse数据集上，相较于cuSPARSE，CSR5和TileSpMV有平均2.98x，2.88x，1.22x的加速比。

负载不均衡和访存不连续是不规则应用在GPU上性能瓶颈的主要原因。有一些研究(例如Efficient Algorithm Design of Optimizing SpMV on GPU)能保证矩阵数据的读取是连续的，并且可在GPU上访存合并，但是对向量x的访问总是不连续的。FastLoad主要是为了解决这个问题设计的算法。

FastLoad使用CSC作为基本的存储格式，提升性能的主要手段有：

  • 根据每列的非零元素数量对列进行排序：主要尽可能保证访存可合并
  • 分块：保证负载尽可能均衡

2 背景

FastLoad是基于CSC存储格式设计的。对于CSC格式，一种基本的并行方式是一列被分配给一个warp。这样一个warp对值的访问是连续的。内存合并访问对于GPU计算的性能是非常重要的，所以FastLoad希望对向量x的访问也是可合并访问的，所以有了分块的设计，后面会详细介绍。

FastLoad为了探索内存合并的性能优化空间，做了一个有趣的假设性实验。一个基本的认识是，CSR格式对于矩阵数据的访问都是可合并的，对于向量x的访问是不连续的，而CSC格式把临时结果写回到向量的时候是无法连续的，如下图所示：

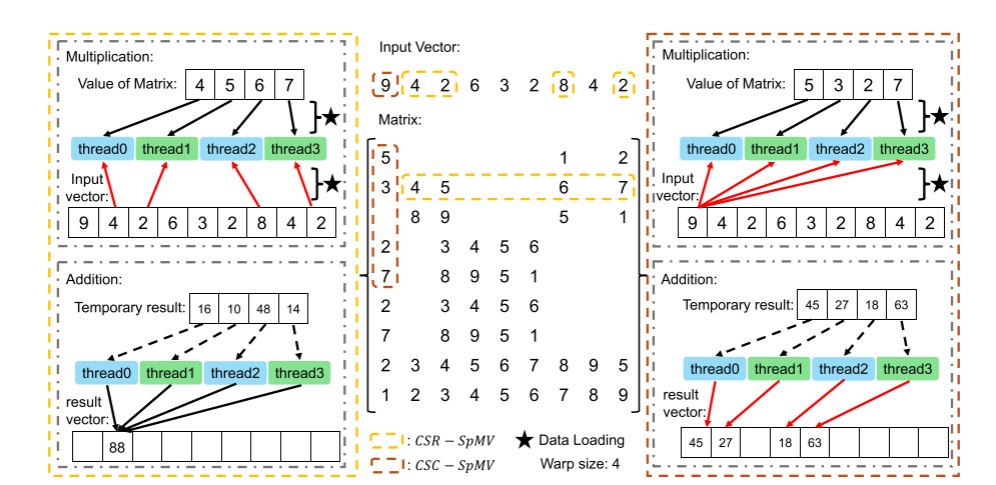
image-20250604193321440

所以FastLoad做了一个实验，按照非零元素对列排序，将宽为32个列的块分配给一个warp，高度则是第一列的非零元素数，这样首先对矩阵数据的访问和对x的访问是连续的，相当于利用了CSC格式的优势。而中间结果是CSC格式，和原矩阵大小应该是完全一样的，在做完这一步之后，将格式转换回CSR格式，做写回的累加，按行写回，这样写回就也是连续的。当然，这只是一个测试访存合并效果的假设实验，因此格式转换的开销没有计入，整体的性能在不计入转换开销的情况下有非常大的提升。

基于上述实验，FastLoad认为合并访存有足够大的性能提升空间，因此尝试在不做格式转换的情况下合并访存。

3 算法设计&实现

3.1 存储结构

FastLoad是基于CSC格式设计的，但需要额外的辅助数组，因为线程warp每次操作的是2D块，所以对矩阵做2D划分需要额外的数据结构。对于块，需要三个额外的数组，一个是==blkColIdx==，记录每个块的起始列号；==blkLength==则是记录了每个块的长度，虽然默认情况下应该是warp线程数，但是不一定有足够的列，因为块的起始列不是对齐的，和元素有关。最后还有一个==blkHeight==，记录块的高度，这个主要是用于计算每个warp需要迭代几轮算完一个块，一般来说是第一列的非零元素数(对列排完序以后第一列是非零元素最少的)，但是有些列可能到最后元素不够了。

对于CSC原有的数据结构，colPtr变成blkPtr了记录块的起始位置，值和索引要调整为以块的单位，并且Z字型排布。如下图所示：

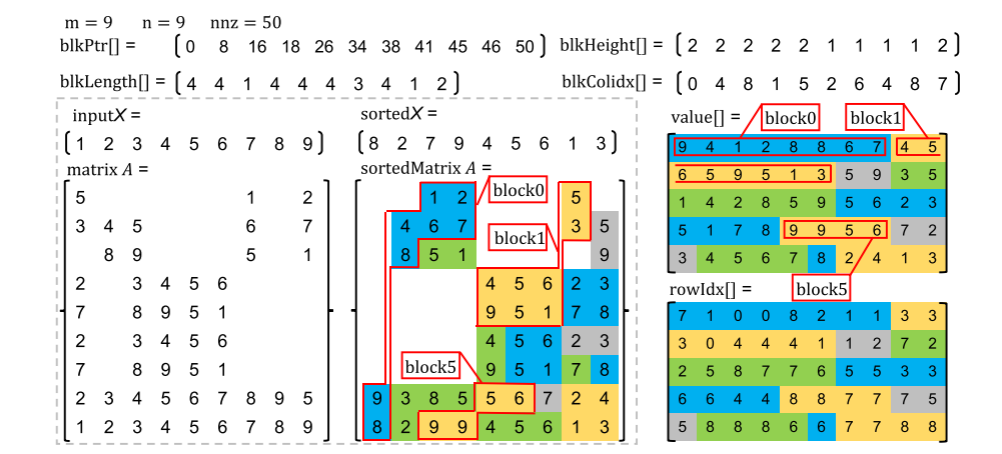
image-20250604200315679

3.2 FastLoad SpMV

FastLoad SpMV和上面的假设实验一样，采用两个阶段的SpMV算法，第一个阶段做数据加载和乘法，第二个阶段做累加和写回，但全程都是基于上述的CSC+额外数组的稀疏矩阵存储结构。在计算的时候通过blkColIdx+laneid来定位当前的列，每个warp会迭代blkHeight轮。

整个算法的第一步是列的排序和块的划分，第二步则是GPU的计算和结果数据的写回。因为每个warp算完的数据可能不是同一行的，所以使用原子加将结果加到对应的结果向量y的位置上，但是原子加随着矩阵的大小增加，效率会很低，所以FastLoad还采用了段求和和前缀和的方式来规约结果。具体而言，根据上图，有一些相邻线程的行索引是相同的，因此可以采用shuffle操作来在warp内实现规约。还有一种可能是warp内的全部元素都是一行的，这种情况下，使用前缀和的方式来求规约结果。

4 总结

FastLoad通过2D分块实现了对矩阵元素和向量都连续进行访问，并且取得了相当优秀的性能，代码也进行了开源，这或许是这篇工作能投稿TPDS的原因。主要的优化思路还是最大化合并内存访问。但是在整篇文章中阅读之后还是有些疑惑，FastLoad和background章节介绍的实验还是有差别的，最后写入y的时候应该仍然是无法保证连续的，论文配图中给出的矩阵其实相对来说比较密集了，每个元素在列方向都有相邻的元素，但在实际情况下如果是高稀疏度的矩阵，应该在行上是完全离散的，所以写回时候的性能仍然是个问题。如果只是前面的计算时候访存的合并就带来了这么大的性能提升，感觉应该之前的工作有做过这样的尝试，不过相较于CSR5，确实在格式上访存更加连续了，这是同样2D块划分的优势。最近没有在做SpMV相关的事了，如果后面有机会，还要好好再研究一下这篇工作。