WISE：Predicting the Performance of Sparse Matrix

Abstract

稀疏矩阵向量乘法(SpMV)是一个重要的稀疏kernel。已经开发了许多方法来加速SpMV。然而，没有一种方法能够在各种矩阵中始终保持最高性能。因此，需要一个性能预测模型来预测给定稀疏矩阵的最佳SpMV方法。不幸的是，由于影响SpMV的因素多种多样，预测SpMV的性能具有挑战性。在这项工作中，作者开发了一个名为WISE的机器学习框架，它可以准确预测给定稀疏矩阵的不同SpMV方法相对于基线方法的加速幅度。 WISE依赖于一个新颖的功能集，该功能集总结了矩阵的大小、偏斜和局部性特征。然后，WISE可以为每个特定矩阵选择最佳的SpMV方法。通过一组近1,500个矩阵，与在24核服务器中使用英特尔MKL相比，使用WISE的平均速度提高了 2.4 倍。

1 Introduction

SpMV是最常用的计算kernel之一。在稀疏线性系统和多种图计算(例如PageRank和HITS(Hyperlink-Induced Topic Search))当中都会使用。许多应用都是迭代使用SpMV kernel，因此SpMV消耗相当多的执行周期，优化SpMV是非常有必要的。

有效执行SpMV的困难在于矩阵的特征复杂，这有时导致SpMV访存局部性很差，并且一些情况下的数据依赖也使优化更难。有许多现有的加速SpMV的方法，采用不同的方式存储矩阵，应对不规则的数据访问及利用SIMD指令。但是没有一种方法对于所有特征的稀疏矩阵都能实现最好性能，因此需要一种选择最好方法的机制。

传统的auto-tuners使用行，列数等基本特征来建立模型，选择方法，但是这对于复杂的不同特征的矩阵不能很好的预测性能。因为SpMV方法在不同的非零元素偏斜和局部性特征下表现不同。

本篇文章，作者使用机器学习建立的一个模型WISE来评估不同SpMV方法在一个矩阵上相对于baseline方法的加速比，从而选择最合适的方法。WISE使用一系列特征来总结矩阵的复杂特征。

作者还考虑了一些优化方法，包括0填充最小化、列重排序、分块。这些优化在流行的SELLPACK，SELL-C-σ，LAV等SpMV实现中使用。

对于偏斜，WISE使用平均值、标准差、基尼指数，以及表示0在行列分布的p-ratio体现特征。对于局部性特征，WISE使用0元素在一个2D子矩阵中的分布统计，以及一些其他统计值来体现。

🔰p-ratio：一种用来描述矩阵的特征之一，它表示矩阵中非零元素在行和列方向上的分布比例。p-ratio可以用来衡量矩阵的平衡性，即数据在行和列方向上的分布是否相等或相近。如果p-ratio为1，说明数据在行和列方向上的分布是均匀的；如果p-ratio大于1，说明数据在行方向上的分布是稠密的；如果p-ratio小于1，说明数据在列方向上的分布是稠密的。

作者分析了一组近 1,500 个不同位置和偏斜行为的矩阵。与在 24 核服务器中使用英特尔数学核心函数库 (MKL) 相比，使用 WISE 的平均加速速度提高了 2.4 倍。此外，WISE 比更先进的 Intel MKL inspector-executor平均加速 1.14 倍，而其预处理开销还不到 50%。得益于 WISE 对用户透明的方法，WISE 可以成为现有数学库的有效扩展。

本篇主要的工作包括：

• 对SpMV性能预测的困难的分析

• 给出一组可用于机器学习模型的描述矩阵的特征

• 实现对给定矩阵选择最佳SpMV方法的框架WISE
• 对WISE进行一系列评估测试

2 Background & SpMV Optimization Space

2.1 CSR Format and SpMV Implementation with CSR

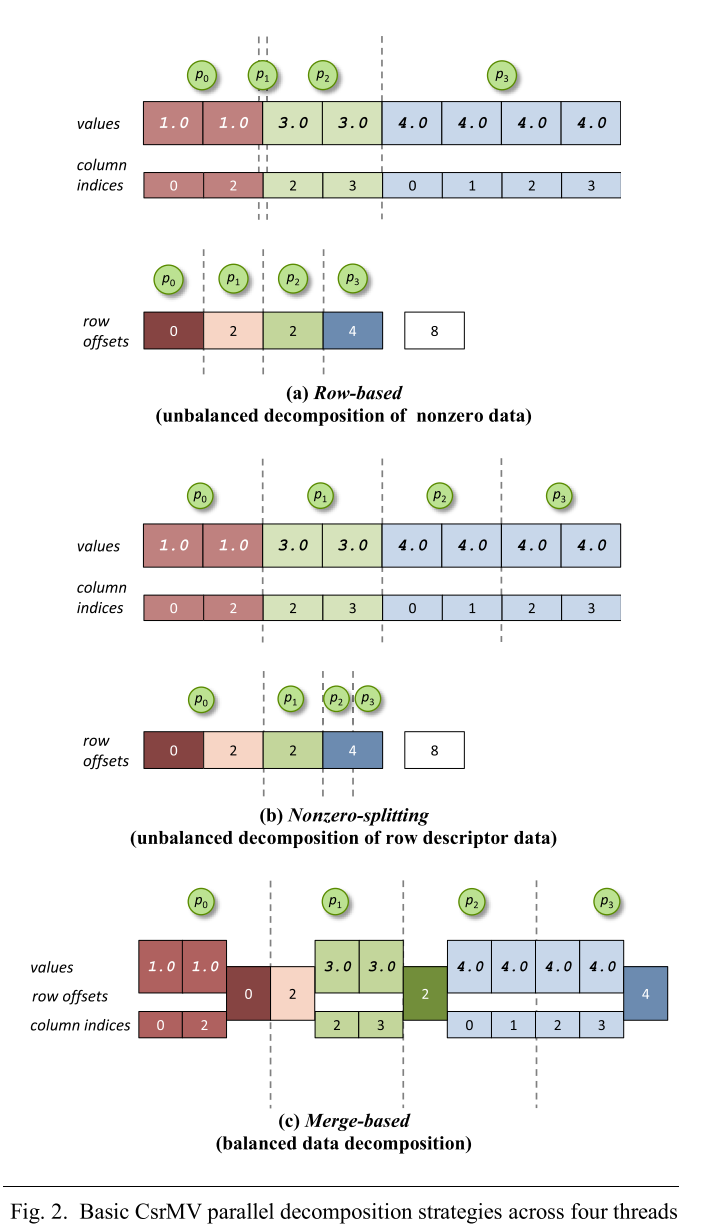
这里作者简单回顾了一下CSR格式，以及CSR以行为粒度并行的负载分配方式(静态交错分配，静态连续分配，动态分配)，就不再赘述了。

2.2 Implementing SpMV with Vectorization

作者考虑了三种向量化优化：

• 减少0填充，方式是通过排序将0元素数相近的行放在一起。
• 列重排序：把非零元素比较多的列放在一起，提高向量访存的局部性
• 分块：将列分块，提高LLC局部性。

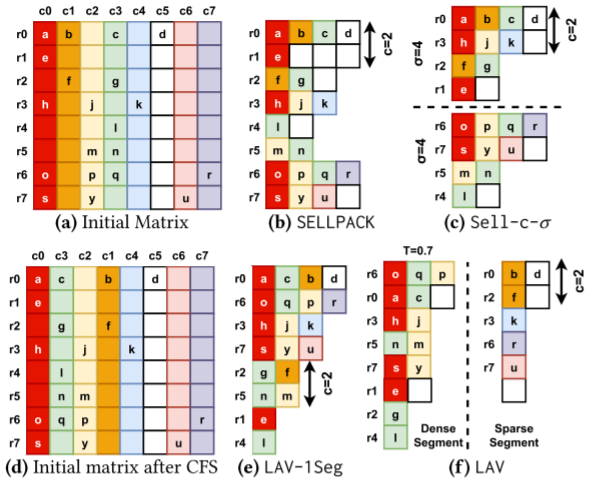
作者选取了三种SpMV的方法，SELLPACK，SELL-C-σ和LAV来分析这些优化。

由于对SELLPACK和SELL-C-σ已经比较了解，这里只重点读了LAV格式。

SELLPACK

SELLPACK把c行作为一个CHUNK，一个CHUNK内的行宽相等，不足的用0填充。c的大小一般是向量长度。当0元素在行之间分布不均匀时，0填充会很多。

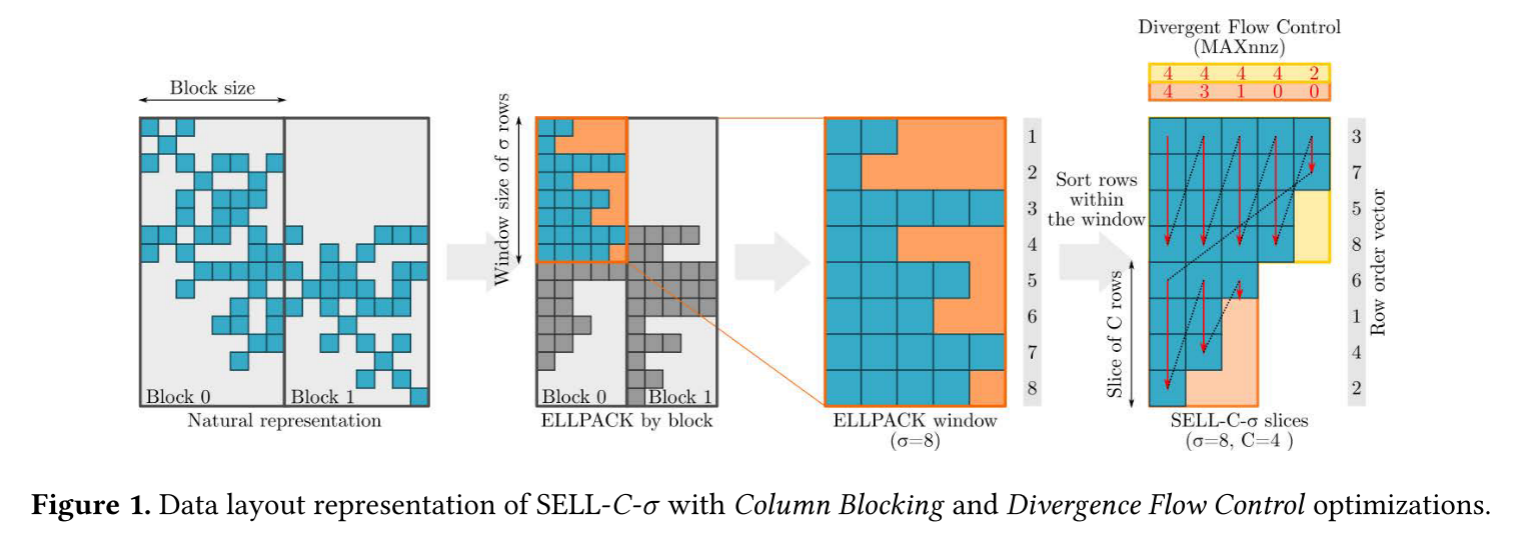
SELL-C-σ

SELL-C-σ对每σ行进行排序，这样能减少0填充，其他概念和SELLPACK一样。σ的最佳取值依赖于非零元素在行之间的分布。如果大多数行的0元素数都差不多，那么σ取较小就可以了，反之需要取较大值。在σ取大一些的情况，需要对许多行重排序，而相邻的行总是有相近的非零元素分布模式，重排序打乱了行顺序，可能导致时间局部性和空间局部性的损失。当nonzero分布非常不平衡时，σ可以取R(row_number)，这样被称为RFS(Row Frequency Reorder)，不过这样就要采用动态调度分配负载，因为靠前的CHUNKnonzero集中。

LAV-1Seg

在幂律图矩阵中，行和列中的零数量高度不平衡。因此，输入向量的时间和空间局部性较差，并且经常遭受LLC缺失。为了解决这个问题，LAV-1Seg(只有一个段的 LAV)根据非零数的递减对列进行排序，这是一种称为列频率排序(CFS)的技术。然后，它应用Sell-c-R的变换。使用 CFS，具有相似非零分布的列通常以紧密的时间顺序进行处理，提高向量x的元素重用。

LAV

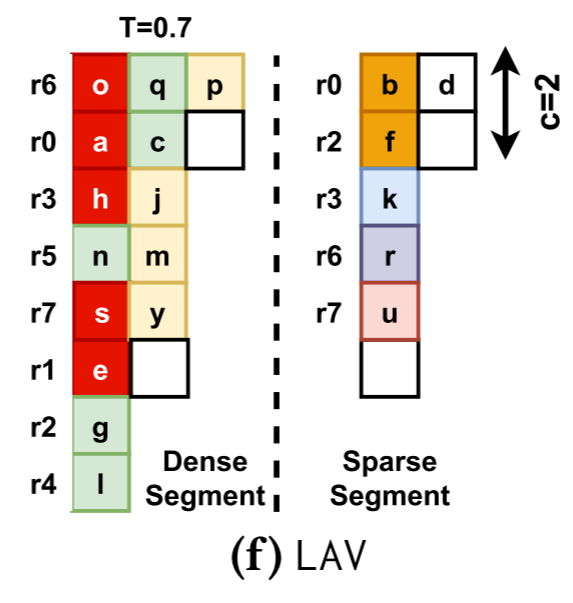
如果矩阵很大，输入向量元素会在重新使用之前从 LLC 中逐出。因此，完整的 LAV 算法采用CFS之后的矩阵，并将其划分为称为段的连续列组。然后，它将Sell-C-R应用于每个段。段应该足够小，以便与该段相对应的输入向量元素适合 LLC 并得到重用。在实践中，LAV通常只需要将矩阵划分为两段。第一段中，取每列非零值的比例为T，最佳T通常≥0.7。它被称为密集段，因为它具有矩阵中填充最多的列。第二段称为稀疏段。

当处理一个段时，相应的输入向量元素被加载到 LLC 中并重用。由于LAV-1Seg和LAV都使用RFS，只选择动态调度。

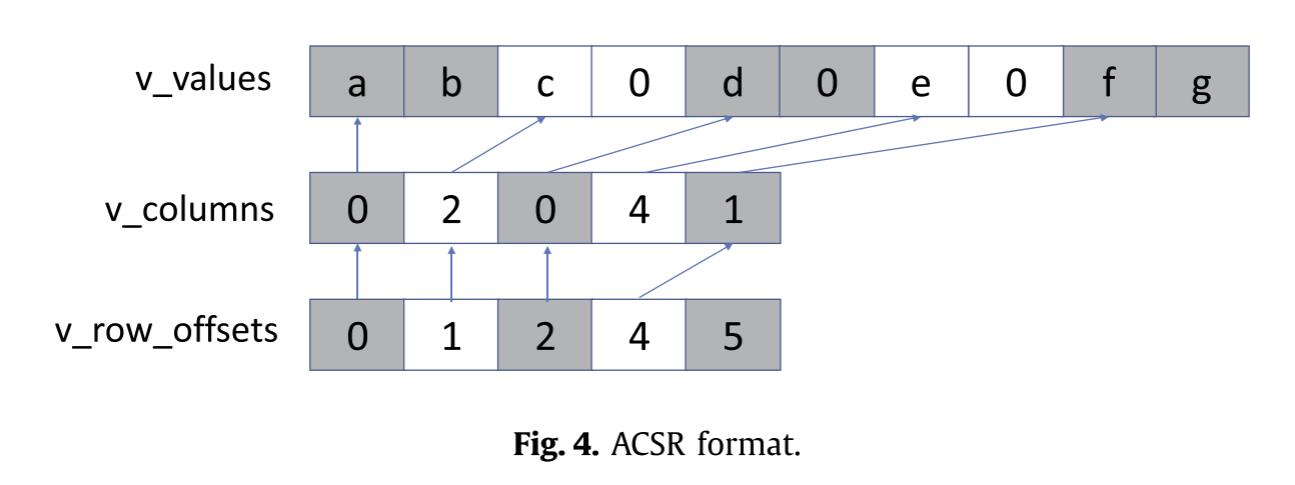
上述这些方法的矩阵格式都不同，作者提出了一个统一的格式来实现SpMV，格式的描述在附录A。

3 Challenges Predicting SpMV Performance

为了选择为每个输入矩阵提供最快 SpMV 执行的方法和参数。作者使用第 2 节中的不同方法和参数在各种矩阵上执行SpMV。

作者使用SuiteSparse矩阵集合中的136个大矩阵和使用RMAT图生成器创建的 408 个大矩阵。SuiteSparse主要包含科学计算矩阵，RMAT 被广泛使用，可以生成广泛的矩阵类型。为了确保矩阵足够大以获得有代表性的结果，作者使用具有 1-6700 万行和列的矩阵。nonzero限制在20亿内以能够在server的内存中存储。

作者的分析提供了五个方面的insight。

最快的方法因矩阵而异

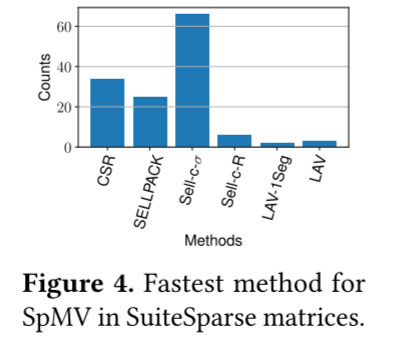
作者在136个矩阵上测试，如图4所示，每个方法在不同数量的矩阵上表现出最好的性能。此外，作者还测试了MKL，MKL没有在任何矩阵实现最佳性能。

同一种方法中，相对CSR的加速比不同(考虑成本)

即使某个方法对于一组矩阵来说是最快的，其实际相对CSR的加速比也有很大差异。如图2所示，1.0是CSR实现的基准，

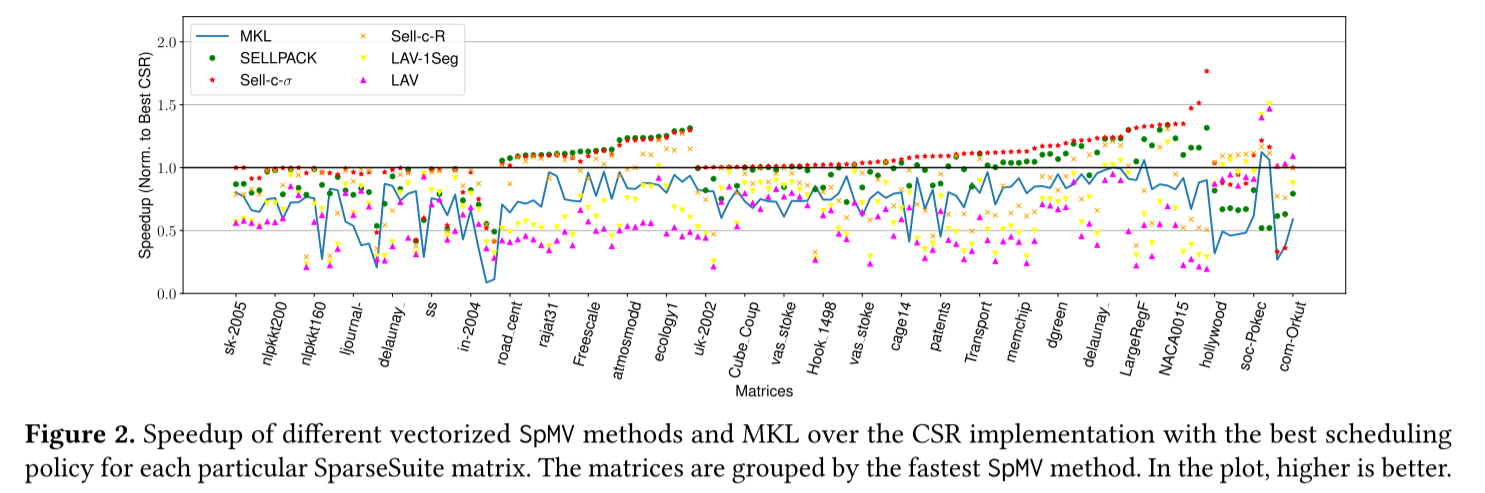
考虑 SELLPACK，它是 25 个连续放置的矩阵中最快的。在这些矩阵中，其加速比范围为 1.05 至 1.31×。另一方面，Sell-c-𝜎 对于 66 个矩阵来说是最快的，对于这些矩阵，加速范围为 1.00 到 1.76×。当稍后考虑方法的预处理成本时，预测加速的幅度可以帮助选择最佳的 SpMV 方法。

选择一种方法的正确参数会显著影响加速比

参数选择会显著影响加速比。例如调度策略。图3显示了使用动态、静态和静态连续调度的CSR实现的性能。对于136个SuiteSparse矩阵中的每一个，该图显示了它们在最佳调度下相对于 CSR 的加速(始终等于或小于 1)。

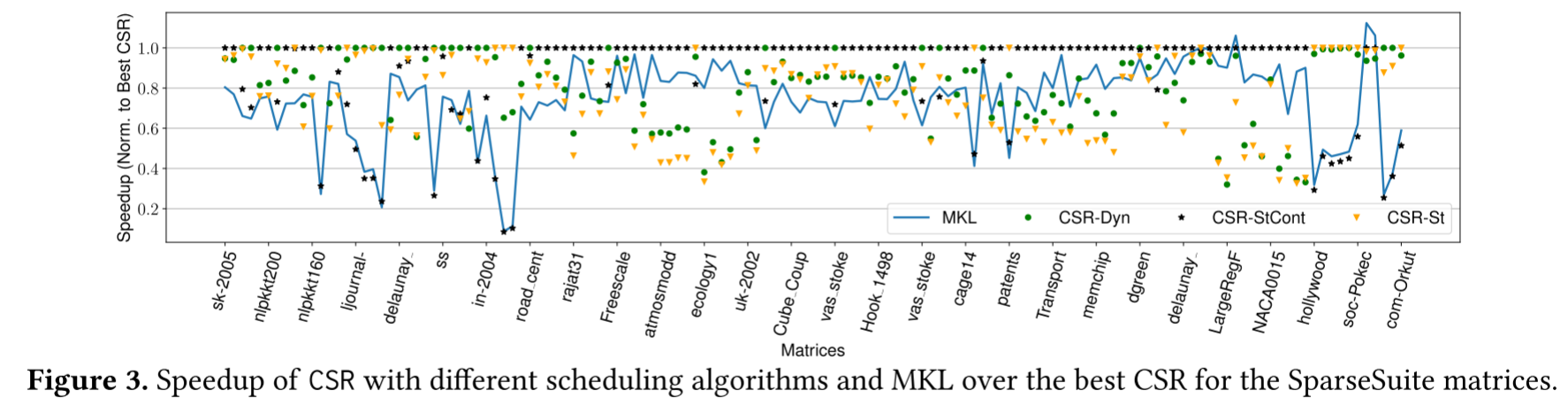
从结果可以分析得到，动态调度对于网络和社交网络来说是最快的，而 静态调度在科学矩阵方面表现最好。该图还显示了MKL的性能。

矩阵大小、局部性和偏斜之间的复杂关系决定了最佳方法

为了分析这三个参数和最佳方法的关联，作者对两个使用RMAT生成的矩阵进行了实验。它们分别显示了nonzero偏斜和nonzero局部性的影响。

在第一个实验中，作者分析了稀疏矩阵的偏斜特性。根据稀疏矩阵行的非零分布来考虑偏斜。使用100个高偏斜(HighSkew，矩阵的非零元素在相对较少的行或列中高度集中)和100个低偏斜(LowSkew)矩阵。在第二个实验中，作者使用100个具有高非零局部性的矩阵(即大多数非零值位于靠近矩阵对角线的区域)(HighLoc)和100个具有低局部性的矩阵(即非零值遍布整个矩阵)(LowLoc)。4.5节描述了使用的 RMAT 参数。在每个 100 矩阵集中，作者改变行数和每行的平均非零值来模拟不同的特征。

首先考虑偏斜的影响。作者测量了第2节中LowSkew和HighSkew集的每个SpMV方法的执行时间。图5a和5b分别显示了LowSkew的最快方法及其相对于最佳CSR的加速。矩阵的特征在于行数和每行非零的平均数(Y 轴)。图5c和5d显示了HighSkew矩阵的相同数据。

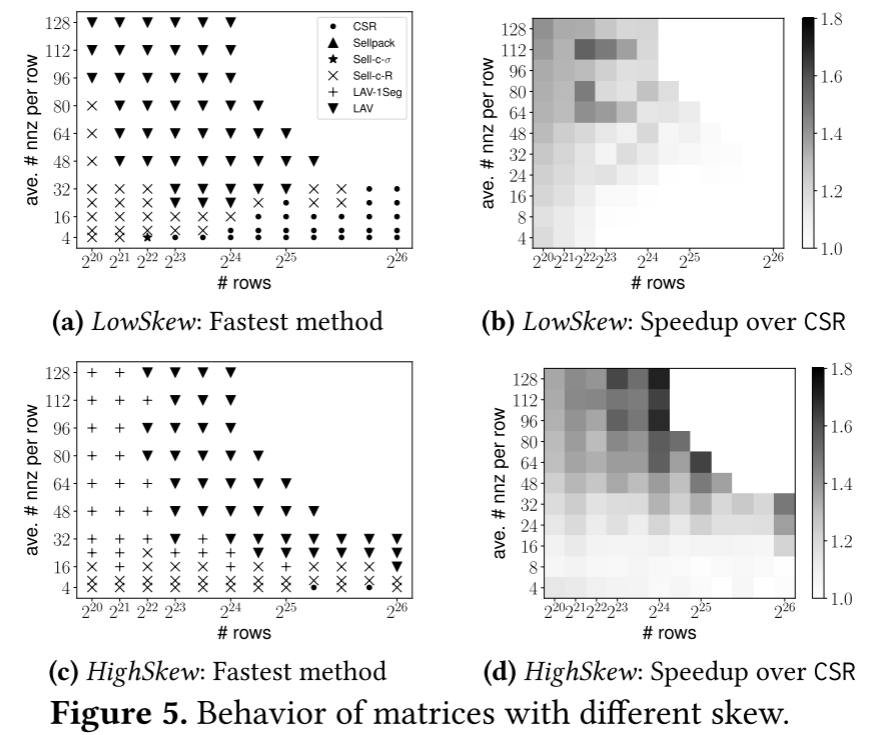
图中可得出LAV(1Seg)，SELL-C-R在大多数情况提供最大加速，当输入矩阵大于LLC(行数>=2^22)，并且每行的平均nnz较高(>16)时，LAV通常优于其他方法。LAV的加速取决于偏斜程度，HighSkew的加速比最高。对于行数较少，nnz较多，偏斜较大的矩阵，LAV-1Seg就够了；而行数较少且偏斜较低时，SELL-C-R通常最快，因为输入向量适合LLC，也不需要更高级的LAV和LAV-1Seg。对于每行平均nnz较低的大型矩阵，加速比很小。

图6展示了LowLoc和HighLoc的数据。SELL-C-σ是处理HighLoc的最好方法，对于LowLoc，SELL-C-σ通常最好，除了每行具有大量nnz的矩阵。这种情况下LAV是最好的，因为提供了分段。最后，HighLoc的Sell-c-𝜎加速幅度高于LowLoc。

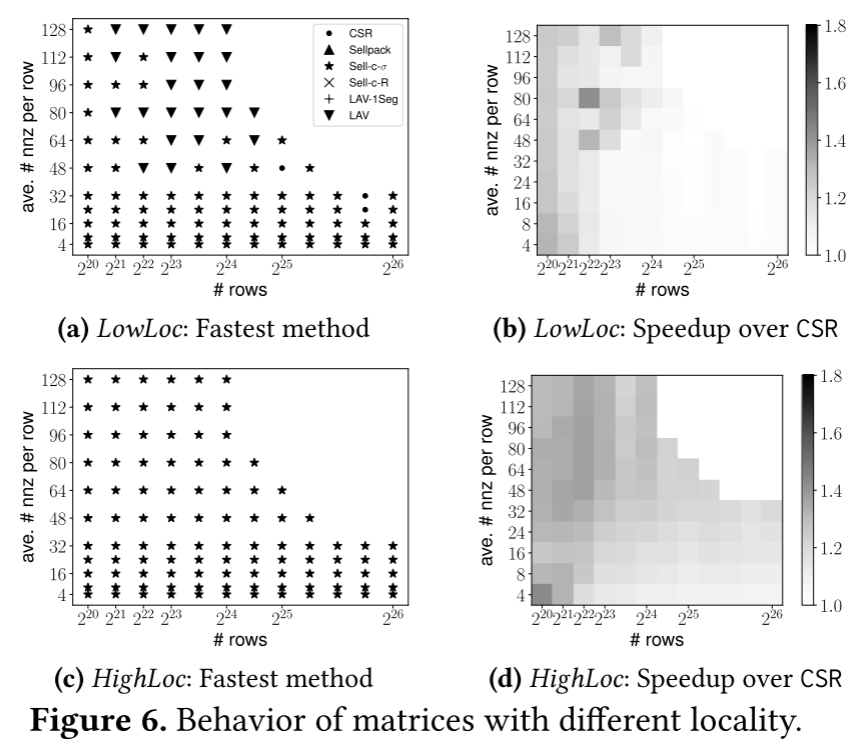
SuiteSparse矩阵没有很多不同的行为

图4显示SparseSuite矩阵中最快的方法通常是Sell-c-𝜎。然而，对图5中RMAT生成的矩阵进行的实验表明，LAV和LAV-1Seg通常是最快的。出现这种差异的原因是SuiteSparse矩阵主要来自科学领域或来自道路图等图；来自幂律图的并不多。

🔰幂率图：节点度(连接数)的分布符合幂律分布。在一个幂率图中，只有少数节点具有非常高的度，而大多数节点的度相对较低。对于一个具有幂律度分布的图，其邻接矩阵可能表现出一些特殊的结构。例如，那些连接度非常高的节点会在矩阵的特定行或列上具有很多非零元素，而大多数节点则在这个矩阵中具有相对较少的非零元素。实际上就是偏斜程度高。

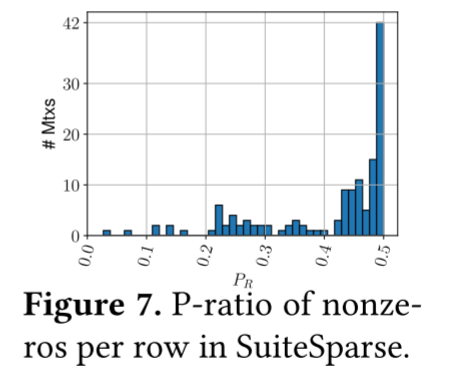
可以通过绘制SuitSparce矩阵中每行非零元素的直方图来观察SuitSparce矩阵。p-ratio表示p比例的行包含了矩阵中(1−p)比例的非零元素。

图7显示了p-ratio的分布。可以看到大多数SuiteSparse矩阵的p-ratio高于0.4。这意味着许多矩阵的非零值到行的分布是平衡的。这一事实使得 SELLPACK和Sell-c-𝜎方法变得有效。此外，SuiteSparse矩阵的列数通常较少。它们中的大多数列数少于5M，允许输入向量适合LLC并减少对 LAV的需求。

总体而言，SuiteSparse更适合Sell-c-𝜎和SELLPACK等方法。如果想使用一组有代表性的矩阵来训练我们的预测模型，需要使用更广泛的矩阵来增强SuiteSparse。

4 WISE: Picking the Best SpMV Method

考虑到为给定输入矩阵选择最佳SpMV方法具有挑战性，作者开发了基于ML的框架WISE，可为给定的稀疏矩阵选择高性能SpMV方法。并设想WISE可以集成到GraphBLAS/BLAS框架中，例如英特尔的MKL。WISE的设计对程序员来说是透明的，并且可以轻松集成到现有系统中。

4.1 Overall Design

WISE由一个新的稀疏矩阵特征集、一组基于ML的性能预测模型以及考虑性能预测模型的输出来选择最佳SpMV方法的启发式算法组成。

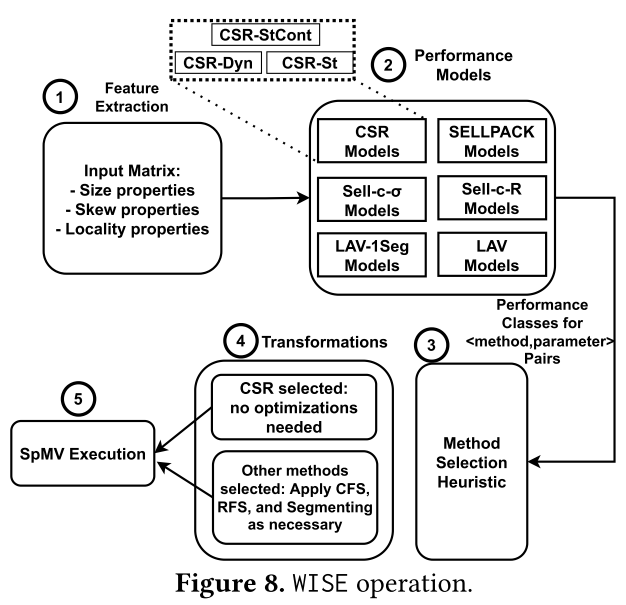
图8展示了WISE的工作过程。

1. WISE从输入矩阵中提取某些特征的值：包括识别稀疏矩阵大小的特征，以及非零分布的偏斜和局部特征。
2. 特征被传递到一组ML性能模型，该模型预测各个方法相对于最佳CSR的加速。
3. 接下来，WISE 选择预计可实现最高加速的方法和参数值，同时包含预处理成本。
4. 将矩阵布局从 CSR 转换为所选方法和参数对的布局。
5. 最后，使用选定的方法、参数和矩阵布局运行SpMV。

4.2 Sparse Matrix Features

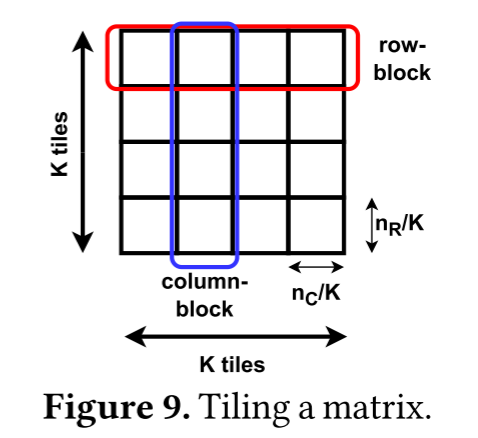
第三节已经分析过，系数矩阵的nnz偏斜及局部性特征影响SpMV的性能。基于此选取性能模型的特征。作者将矩阵划分为K^2块，每块nR/K行，nC/K列。基于系数矩阵的大小和L2缓存的大小，选取K=2048。作者将块的行和列分别称为行块和列块(图 9)。然后考虑nnz在行(R)、列(C)、块(T)、行块(RB)和列块(CB)上的分布。

为了表征每个分布，作者使用平均值(𝜇)、标准差(𝜎)、方差(𝜎2)、最小值、最大值、基尼系数(G)和p-ratio(P)。G和P是计算分布中不平衡的统计度量。在最不平衡分布中(即所有非零值都在一个桶中)，G接近1，P接近0。完美平衡分布G=0且P=0.5。此外，还记录不为零的桶的数量(ne)。作者使用stat_dist作为这些统计量的命名约定，其中stat是汇总统计量的名称，dist是分布名称(R、C、T、RB和CB)。

接下来，描述如何使用这些汇总统计数据和附加统计数据为基于ML的性能预测器创建稀疏矩阵特征。表2显示了WISE从输入矩阵中提取的特征，分为矩阵大小、非零偏斜和非零局部性。

(1)矩阵大小性质

WISE测量行数nR、列数nC和非零数。nC给出有关输入向量大小的信息，而非零数给出有关要完成的工作量的信息。

(2)非零偏斜性质

WISE使用测量行和列之间非零分布的偏斜程度的特征。收集的统计数据列于表2中。行分布的特征决定了矢量化的行调度和填充。 列分布的特征决定了对输入向量的内存访问的不规则性。因此，它们可以表明CFS在LAV-1Seg和LAV中的有效性。

(3)非零元素局部性性质

WISE使用T、RB和CB分布来捕获非零局部性特征，例如，T分布中的低p-ratio表明非零值集中在几个块中。因此，SpMV的内存访问具有较高的局部性。

WISE还收集了每个块内非零元素布局的信息。对于块i，uniqRi和uniqCi分别是包含非零元素的行数和列数。如果许多非零元素在同一行或同一列，那么访问就有可能利用局部性。此外，由于数据按照缓存行排列，如果非零元素相邻，它们可能共享缓存行并进一步增强局部性。因此，WISE还测量了块𝑖的GrX_uniqRi和GrX_uniqCi，它们是按照X个相邻行(或列)分组的包含非零元素的行数和列数。例如，如果𝑋=16，那么16个相邻的列(或行)将计为一个ID。WISE使用{4, 8, 16, 32, 64}这些值作为X。为了理解它们的用途，考虑64字节的缓存行。在这种情况下，一行可能容纳四个128位的元素(我们对𝑋=4感兴趣)或八个64位的元素(我们对𝑋=8感兴趣)。如果在相近的时间内访问了缓存行中的多个元素，我们就可以得到一个缓存命中。

WISE获取每个块的uniqRi，uniqCi，GrX_uniqRi , 和GrX_uniqCi。然后，它将所有块的这些值求和，并除以矩阵中的非零元素个数。得到的值，我们称之为uniqR，uniqC，GrX_uniqR和GrX_uniqC，被用作矩阵的特征。

最后，WISE测量每一行𝑖中至少有一个非零元素的块数(potReuseRi)。它也测量每一列𝑖的类似指标(potReuseCi)。如果这些指标很高，那么在LLC中有数据重用的潜力，因为数据在不同的块之间被重用。另外，WISE测量每𝑋个连续行的组𝑖中至少有一个非零元素的块数(GrX_potReuseRi)。对于每𝑋个连续列的组𝑖，它也测量一个类似的指标，叫做GrX_potReuseC𝑖。最后，WISE将这些测量值在所有行(potReuseR)、所有列(potReuseC)、所有𝑋个连续行的组(GrX_potReuseR)和所有𝑋个连续列的组(GrX_potReuseC)上求平均。这些平均值被用作矩阵的特征。

注意，R，C，T，RB和CB的分布不是用来训练基于机器学习的性能预测模型的特征。使用从分布中计算出的汇总统计量作为训练特征。

4.3 Performance Prediction Models

WISE使用决策树作为性能模型。因为每个特征都有不同的取值范围，难以归一化到一个范围。例如行列数可以高达百万但Gini-index只在0-1之间。

不同方法和对应参数之间产生多种组合，因此性能预测模型有共29个。

• CSR：三种不同调度
• SELLPACK：静态连续和动态调度 + c的取值
• SELL-C-σ：静态连续和动态调度 + c的取值 + σ的取值
• SELL-C-R/LAV-1Seg：动态调度 + c的取值
• LAV：动态调度 + c的取值 + T的取值

以上所有c的取值都为{4,8}，为向量指令的长度。σ为{2^9,2^12,2^14}，2^9符合L1的大小，2^14符合L2的大小。T的取值为{0.7,0.8,0.9}，覆盖不同程度的nnz偏斜。

对于决策树可能会遇到的过拟合问题，作者将树的最大深度限制为 15，以避免创建仅包含少量样本的分支。并启用最小成本复杂度修剪，阈值为 0.005。树的最大深度和修剪阈值是使用网格搜索通过实验选择的。此外，决策树使用基尼系数作为分割标准。

加速比分类

每个模型都会预测相对于最快 CSR 方法的方法和参数值组合的执行时间。每个模型输出7个类(C0-C6)，对应7个执行时间范围。C0 = (∞ - 1.05], C1 = (1.05 - 0.95], C2 = (0.95 - 0.85], C3 = (0.85 - 0.75], C4 = (0.75 - 0.65], C5 = (0.65 - 0.55], C6 = (0.55 - 0]。C0 包括使用给定方法减速的所有矩阵，C6 包括加速超过 2 倍的所有矩阵。值低于 1 的类别表示加速。

4.4 Choosing the SpMV Method

WISE会选择产生最大加速比的方法和参数对。如果有接近的，WISE会选择最小预处理开销的。预处理开销从低到高为：CSR, SELLPACK, Sell-c-𝜎, Sell-c-R, LAV-1Seg, LAV。而参数则从小到大选取，因为小参数预处理时间更少。

4.5 Creating a Representative Training Set

机器学习模型需要具有代表性的训练集来执行预测。但第三节的分析表明SuitSparse中的矩阵没有很多不同的行为，因此作者使用了RMAT生成的一组矩阵补充。

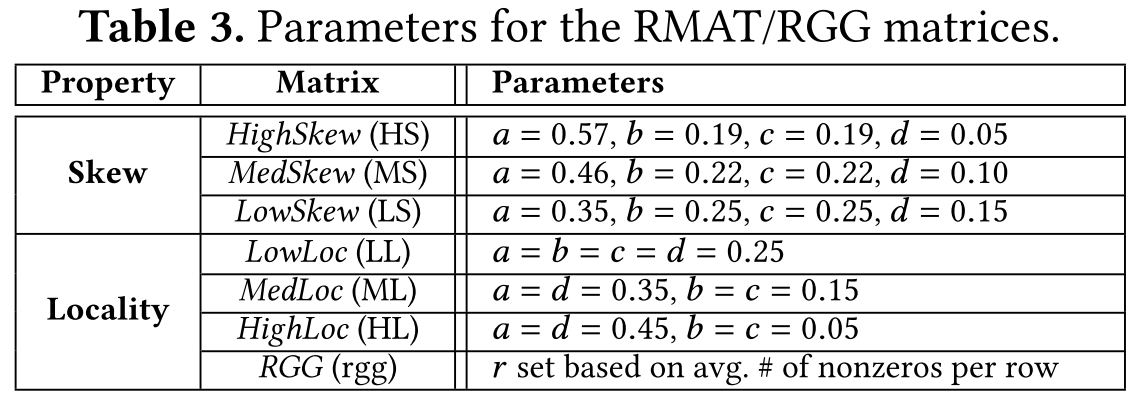
RMAT 生成器有 3 个参数：节点数；平均节点度；边落入四个象限中每个象限的概率a，b，c，d。为了放置边，根据概率选择矩阵的象限。选定的象限再次分为四个象限，并且重复该过程直到最终形成单个矩阵单元。

为了获得偏斜矩阵，作者从Graph500参数开始，即 a=0.57、b=0.19、c=0.19 和 f=0.05(HighSkew)。他们生成幂律图。然后，减少a参数，同时增加b,c和d，以减少偏斜，同时仍然创建community structure(a>d)。分析两种图形类型，参数为 𝑎=0.46、𝑏=0.22、𝑐=0.22 和 𝑑=0.10(MedSkew)，以及a=0.35、b=0.25、c=0.25 和 d=0.15 (LowSkew)。 HighSkew、MedSkew 和 LowSkew 图的行非零分布的p-ratio分别为 ≈0.1、≈0.2、≈0.3。

🔰community structure：指图中的节点可以被划分为若干个子集，每个子集内部的节点之间有较多的连接，而不同子集之间的节点之间有较少的连接。社区结构可以反映图中的一些潜在的模式或特征，例如社交网络中的兴趣群体，知识图谱中的语义类别，网络流量中的异常行为等。幂律图可以用四个参数a,b,c,d来描述，它们分别表示从一个节点出发，到达同一个社区，相邻社区，相邻社区的相邻社区，或者其他社区的概率。一般来说，a越大，表示同一个社区内部的连接越多，社区结构越明显；d越大，表示不同社区之间的连接越多，社区结构越模糊。

为了获得具有不同局部性的矩阵，从a=b=c=d=0.25(Erdos-Renyi)(LowLoc)开始，其中非零值均匀分布在所有列和行上。作者通过等量地增加a和d参数并以相同的量减少b和c来获得非零值聚集在对角线周围的矩阵。使用MedLoc(a=d=0.35, b=c=0.15)和HighLoc(a=d=0.45, b=c=0.05)，局部性上升。对于LowLoc、MedLoc和HighLoc图，行非零分布的p-ratio为0.4-0.5，显示出很小的偏差。

除了RMAT图，作者还加入了一些随机几何图(RGG)。RGG是无向空间图，在二维网格随机均匀放置n顶点来生成，如果两个顶点在网格中的距离小于r，就用一条边连接他们，r设置为：

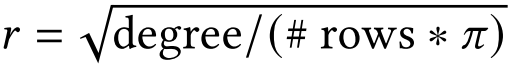
其中degree是随机图的期望平均度数。作者使用RGG图来模拟具有空间结构的矩阵的行为。RGG图具有高度的局部性。

5 Experimental Setup

测试机器为2.6GHz的Intel Gold 6126 Skylake。处理器有两路，每路12核。每核32KB L1和1MB L2，每一路有一个共享19MB LLC。有192GB主存。使用4/8宽的向量指令。

为了训练和测试WISE，作者使用SuiteSparse中的136个矩阵和第4.5节中所述图生成的1326个矩阵。对于SuiteSparse矩阵，使用具有2^20-2^26行的大型矩阵，但非零值少于20亿个，以适应单台机器的内存。对于RMAT和RGG矩阵，使用具有2^20、2^21、2^22、2^23、2^24、2^24.58、2^25、2^25.30、2^25.58、2^25.80和2^26行的矩阵，每行的平均非零数为4-128。每个矩阵使用的非零总数不超过20亿个。

作者使用C++和OpenMP来实现并行性。依靠 OpenMP simd pragma进行矢量化。使用带有O3和vec标志的Intel编译器v2021。在执行过程中，运行24个线程，这些线程都固定到物理核心。使用numactl -i all在NUMA节点之间交错内存分配。

测试时作者采用k-fold，取k=10测试。

6 Experimental Results

6.1 Characteristics of the Matrix Set

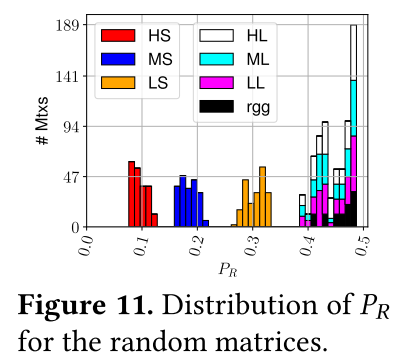
补充的RMAT矩阵和RGG矩阵使矩阵集更具代表性。原因有两个方面，首先是非零偏斜，通过随机矩阵中每行非零值的p-ratio分布来测量。图11中所示的这种分布应与图7中的 SuiteSparse 矩阵的分布进行对比。与图7不同。HS、MS 和 LS 的p-ratio值分别为 0.1、0.2和0.3。选择用于建模不同局部性特征的矩阵的p-ratio值约为≈0.4-0.5，这能够在不受偏斜行为干扰的情况下对局部性效果进行建模。

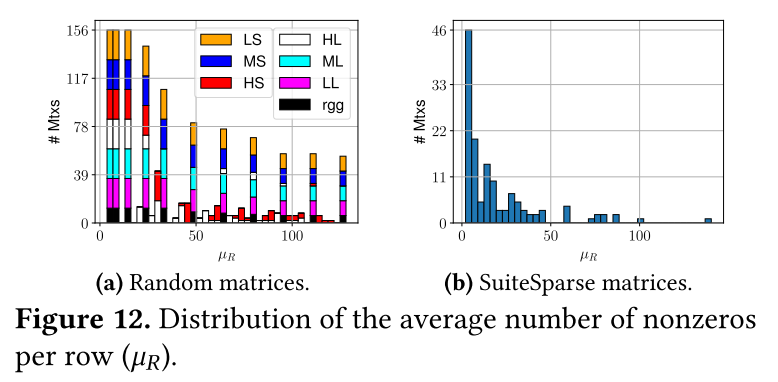
第二个方面是每行非零的平均数量(μR)的分布，即在图中，节点的平均度数的分布。图12显示了随机矩阵和 SuiteSparse 矩阵的这种分布。可以看到随机矩阵涵盖了更广泛的 𝜇𝑅 值范围。随机矩阵集合包括具有较大𝜇𝑅值的矩阵，这导致向量单元的利用率更高。总体而言，两组矩阵的组合能够训练更有效的机器学习模型。

6.2 Classification Accuracy of WISE

图10显示了WISE对加速区间预测的准确性。显示了五个代表型模型的矩阵。所有模型的c=8。垂直轴是正确的类别，水平轴是预测的类别。

相邻类的性能间隔是10%，可以看到大多数预测类和正确类之间的距离在0-1之间，意味着大部分WISE估计值在正确执行时间的10%以内。具体来说，WISE对于SELLPACK、Sell-c-𝜎、Sell-c-R、LAV-1Seg和LAV的准确率分别为87%、92%、87%、84%和83%。此外，在分类错误的矩阵中，大多数分类与正确类别的距离仅一。这样的矩阵分别占SELLPACK、Sell-c-𝜎、Sell-c-R、LAV-1Seg和LAV错误分类矩阵的94%、89%、90%、91%和92%。一般来说，高估和低估加速比的矩阵数量是相当的。

未显示的其他模型的结果与图 10 中的结果相当。总的来说，可得出结论，WISE 可以高精度预测不同方法的加速。

6.3 WISE: Speedup and Preprocessing Overhead

图13a显示了在所有矩阵的MKL基准上使用 WISE 获的加速分布。

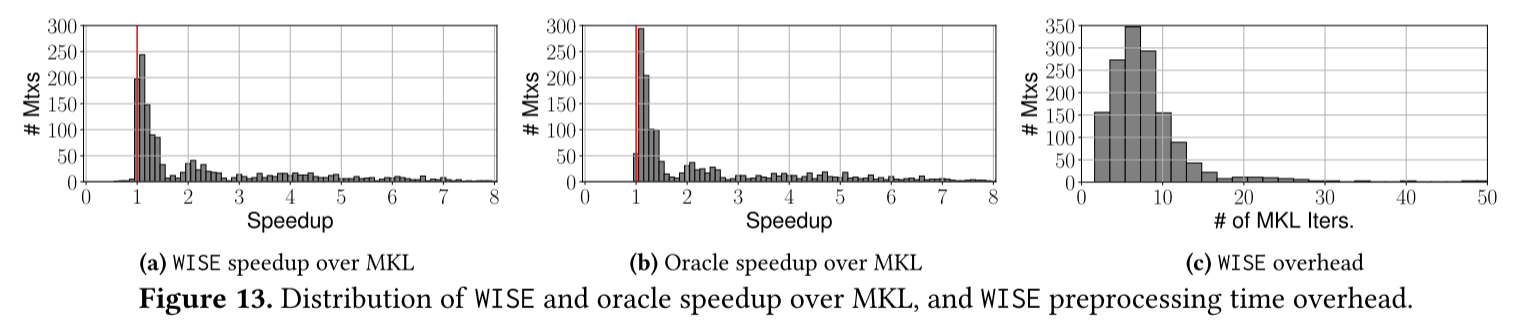
WISE对大多数矩阵都有加速效果，最高可达4-8x，平均加速比是2.4x。13b展现了选择每个矩阵对应最快的方法的加速比，平均加速比是2.5x，WISE的结果与之非常相近。

这些加速数字不包括预处理时间开销。后者由CSR的格式转换和特征计算组成。图13c显示了WISE预处理时间开销的分布。以花费相同时间的MKL的SpMV迭代次数来报告开销。从图中可以计算出WISE的平均开销为8.33次MKL SpMV迭代。

6.4 Comparison to MKL Inspector-Executor

接下来作者还与Intel的MKL inspector-executor(IE)进行了比较。IE也会在许多方法中选择最合适的，但是具体细节是隐藏的。MKL IE可以减少SpMV的时间，但是会带来高昂的预处理开销。

作者测量后，发现MKL IE有平均相对与MKL基本方法的2.11x加速比，不包括预处理时间，而预处理时间为17.43MKL SpMV迭代。因此WISE的加速比相对于MKL IE为1.14x，并且预处理时间也比MKL IE少50%。

6.5 Choosing Decision Tree Parameters

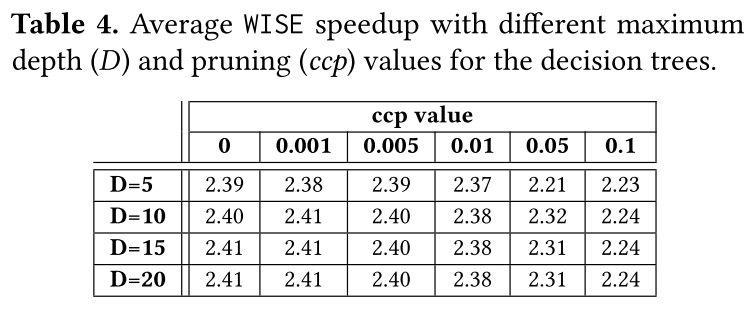
决策树中的两个重要参数是树的最大深度D和修剪程度ccp_alpha(缩写为ccp)。对于D，作者测试{5, 10, 15, 20}值；对于ccp，测试{0, 0.001, 0.005, 0.01, 0.05, 0.1}值。表4显示了WISE在具有不同D和ccp值的MKL上获得的平均加速。可以得出ccp应该很低(即低于0.05)，而D应该很高(即10或更高)。总的来说，为WISE选择D=15和ccp=0.005。

7 Related Work

之前的一些工作已经使用自动调整来加速稀疏矩阵运算。此类系统每次处理矩阵时都会增加潜在的高自动调整开销。使用WISE，创建模型后，每个矩阵的预处理开销很小。

之前的其他工作已经利用机器学习进行方法选择，即选择为给定稀疏矩阵提供最高性能的方法。 WISE 与之前的工作有两个不同之处。首先，WISE中ML模型的输出不是SpMV方法；它是给定方法的潜在加速。结果是一个可扩展的框架，可以在不改变现有模型的情况下添加新方法。其次，WISE不仅考虑给定方法，而且还考虑给定方法的参数。例如，WISE选择给定c和T参数值的 LAV 方法。

赵等人[43]使用一种新颖的汇总技术，将稀疏矩阵表示为小二维图像。然后，他们在该图像上使用 CNN 来确定矩阵的最佳格式。 WISE也使用矩阵的2D块表示。然而，它用它来建模矩阵的局部特征。此外，WISE使用决策树作为ML模型，并使用大一个数量级的矩阵来训练和测试ML模型。

一些方法(例如，SMAT [23])使用由实际使用的SpMV方法驱动的ML特征。例如，一些特征是所使用的特定矩阵格式的存储器开销。相比之下，WISE选择作为ML模型输入的特征不受所使用的 SpMV 方法的影响。

SpMV和图处理的局部优化示例有很多。例如，Cagra[42]预处理一个图，将其划分为较小的 LLC 大小的子图。其他示例包括分箱技术[4, 8]。对于所有这些技术，WISE可以通过新的性能模型进行扩展。 Milk[19]是一组语言扩展，旨在提高间接内存访问的局部性，也可用于SpMV计算。还有编译时和运行时技术来加速具有间接内存访问的程序[31, 33]。此外，分区技术也可以用来改善局部性[10]。

之前的工作目标是重新标记图的顶点以提供更好的局部性[2,3,6,37]。这些技术实现了高局部性，但会产生大量开销。在这项工作中，我们只考虑RFS和CFS重新排序机制。然而，WISE 可以作为第一步来决定是否应用更先进的重新排序技术，从而可能消除开销。

已经提出了许多不同的SpMV向量化方法[12,21,24,25,32,38]。他们的主要目标是最大化向量单元的利用率。刘等人[25]建议使用有限窗口排序，它与 RFS 类似，但只考虑一小部分行。 VHCC[32]设计了一种2D锯齿状格式，用于SpMV的有效向量化。WISE的功能可以有效评估这些技术的潜力。

8 Conclusions

为了加速SpMV，本文开发了一个名为WISE的ML框架，该框架可以预测给定稀疏矩阵的不同SpMV方法相对于baseline方法的加速幅度。 WISE依赖于一个新颖的特征集，该特征集总结了矩阵的大小、非零偏斜和非零局部性。 WISE能够以高精度选择最佳的SpMV方法及其参数。对于一组近1,500个矩阵以及几种流行的方法和优化，WISE在24核服务器中实现了比英特尔MKL平均2.4倍的加速。此外，WISE 的平均加速比英特尔的MKL IE提高了1.14倍，而其预处理开销还不到50%。得益于WISE对用户透明的方法，具有更多方法和优化的扩展WISE是对MKL等GraphBLAS/BLAS库的有效补充。

Appendix A：Unified Matrix Format

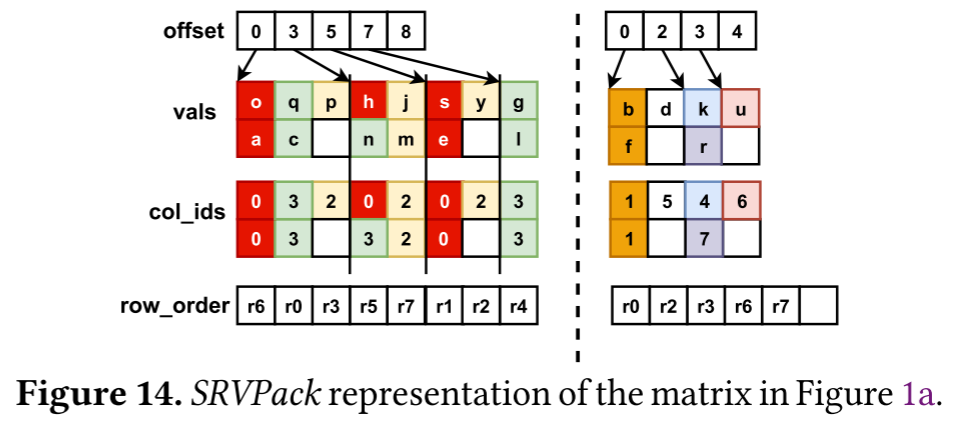
为了能够快速提取出各种格式向量化计算的信息，作者提出了一个矩阵表示格式，称为Segmented Reordered Vector Packing(SRVPack)。

SRVPack支持将矩阵数据分为LAV中提到的两段(segment)，密集的段和稀疏的段。每一部分都存储RFS+SELL-C-R格式的数据。每个segment有一个row_order数组记录新的行顺序。每个Chunk内的行按row_order顺序存储，行长度不足Chunk宽度的进行0填充。类似CSR，有一个val数组存储元素和一个col_id存储列号。这些二维数组有一个长度为c的Y维，一个长度为segment中的Chunk总长的x维，另外有一个offset数组存储每个Chunk的第一个nonzero元素。创建这种统一格式的开销是预处理开销的一部分。

References

[1] Walid Abu-Sufah and Asma Abdel Karim. 2013. Auto-tuning of Sparse Matrix-Vector Multiplication on Graphics Processors. In Supercomputing, Julian Martin Kunkel, Thomas Ludwig, and Hans Werner Meuer (Eds.). Springer Berlin Heidelberg, Berlin, Heidelberg, 151–164.
[2] R. C. Agarwal, F. G. Gustavson, and M. Zubair. 1992. A high performance algorithm using pre-processing for the sparse matrix-vector multiplication. In Supercomputing ’92:Proceedings of the 1992 ACM/IEEE Conference on Supercomputing. 32–41.
[3] J. Arai, H. Shiokawa, T. Yamamuro, M. Onizuka, and S. Iwamura. 2016. Rabbit Order: Just-in-Time Parallel Reordering for Fast Graph Analysis. In 2016 IEEE International Parallel and Distributed Processing Symposium (IPDPS). 22–31. https://doi.org/10.1109/IPDPS.2016.110
[4] S. Beamer, K. Asanovic, and D. Patterson. 2017. Reducing Pagerank Communication via Propagation Blocking. In 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS). 820–831. https://doi.org/10.1109/IPDPS.2017.112

[5] Scott Beamer, Krste Asanovic, and David A. Patterson. 2015. The GAP Benchmark Suite. CoRR abs/1508.03619 (2015). arXiv:1508.03619 http://arxiv.org/abs/1508.03619
[6] Paolo Boldi, Marco Rosa, Massimo Santini, and Sebastiano Vigna. 2011. Layered Label Propagation: A Multiresolution Coordinate-free Ordering for Compressing Social Networks. In Proceedings of the 20th International Conference on World Wide Web (Hyderabad, India) (WWW ’11). ACM, New York, NY, USA, 587–596. https://doi.org/10.1145/1963405.1963488
[7] Sergey Brin and Lawrence Page. 1998. The Anatomy of a Large-scale Hypertextual Web Search Engine. Comput. Netw. ISDN Syst. 30, 1-7 (April 1998), 107–117. https://doi.org/10.1016/S0169-7552(98)00110-X
[8] Daniele Buono, Fabrizio Petrini, Fabio Checconi, Xing Liu, Xinyu Que, Chris Long, and Tai-Ching Tuan. 2016. Optimizing Sparse Matrix-Vector Multiplication for Large-Scale Data Analytics. In Proceedings of the 2016 International Conference on Supercomputing (Istanbul, Turkey) (ICS ’16). ACM, New York, NY, USA, Article 37, 12 pages. https://doi.org/10.1145/2925426.2926278
[9] Alfredo Buttari, Victor Eijkhout, Julien Langou, and Salvatore Filip-pone. 2007. Performance Optimization and Modeling ofBlocked Sparse Kernels. Int. J. High Perform. Comput. Appl. 21, 4 (Nov. 2007), 467–484. https://doi.org/10.1177/1094342007083801
[10] U. V. Catalyurek and C. Aykanat. 1999. Hypergraph-partitioning-based decomposition for parallel sparse-matrix vector multiplication. IEEE Transactions on Parallel and Distributed Systems 10, 7 (July 1999), 673–693. https://doi.org/10.1109/71.780863
[11] Deepayan Chakrabarti, Yiping Zhan, and Christos Faloutsos. 2004. R-MAT: A Recursive Model for Graph Mining. In Proceedings of the 2004 SIAM International Conference on Data Mining (SDM). 442–446. https://doi.org/10.1137/1.9781611972740.43
[12] Linchuan Chen, Peng Jiang, and Gagan Agrawal. 2016. Exploiting Recent SIMD Architectural Advances for Irregular Applications. In Proceedings of the 2016 International Symposium on Code Generation and Optimization (Barcelona, Spain) (CGO ’16). ACM, New York, NY, USA, 47–58. https://doi.org/10.1145/2854038.2854046
[13] Intel Corp. 2015. Intel Math Kernel Library Inspector-executor Sparse BLAS Routines. https://software.intel.com/en-us/articles/intel-math-kernel-library-inspector-executor-sparse-blas-routines.
[14] Intel Corp. 2015. Sparse BLAS CSR Matrix Storage Format. https://www.intel.com/content/www/us/en/develop/documentation/onemkl-developer-reference-c/top/appendix-a-linear-solvers-basics/sparse-matrix-storage-formats/sparse-blas-csr-matrix-storage-format.
[15] Timothy A. Davis and Yifan Hu. 2011. The University ofFlorida Sparse Matrix Collection. ACMTrans. Math. Softw. 38, 1, Article 1 (Dec. 2011), 25 pages. https://doi.org/10.1145/2049662.2049663
[16] Daniel Funke, Sebastian Lamm, Ulrich Meyer, Peter Sanders, Manuel Penschuck, Christian Schulz, Darren Strash, and Moritz von Looz. 2019. Communication-free Massively Distributed Graph Generation. J. Parallel and Distrib. Comput. 131, C (2019).
[17] Eun-Jin Im, Katherine Yelick, and Richard Vuduc. 2004. Sparsity: Optimization Framework for Sparse Matrix Kernels. The International Journal of High Performance Computing Applications 18, 1 (2004), 135–158. https://doi.org/10.1177/1094342004041296 arXiv:https://doi.org/10.1177/1094342004041296
[18] Z. Jia, L. Wang, J. Zhan, L. Zhang, and C. Luo. 2013. Characterizing data analysis workloads in data centers. In 2013 IEEE International Symposium on Workload Characterization (IISWC). 66–76. https://doi.org/10.1109/IISWC.2013.6704671
[19] Vladimir Kiriansky, Yunming Zhang, and Saman Amarasinghe. 2016. Optimizing Indirect Memory References with Milk. In Proceedings of the 2016 International Conference on Parallel Architectures and Compi-lation (Haifa, Israel) (PACT’16). ACM, New York, NY, USA, 299–312. https://doi.org/10.1145/2967938.2967948

[20] Jon M. Kleinberg. 1999. Authoritative Sources in a Hyperlinked Environment. J. ACM 46, 5 (Sept. 1999), 604–632. https://doi.org/10.1145/324133.324140
[21] Moritz Kreutzer, Georg Hager, Gerhard Wellein, Holger Fehske, and Alan R. Bishop. 2014. A Unified Sparse Matrix Data Format for Efficient General Sparse Matrix-Vector Multiplication on Modern Processors with Wide SIMD Units. SIAM Journal on Scientific Computing 36, 5 (Jan 2014), C401–C423. https://doi.org/10.1137/130930352
[22] Jérôme Kunegis and Julia Preusse. 2012. Fairness on the Web: Alternatives to the Power Law. In Proceedings of the 4th Annual ACM Web Science Conference (Evanston, Illinois) (WebSci ’12). Association for Computing Machinery, New York, NY, USA, 175–184. https://doi.org/10.1145/2380718.2380741
[23] Jiajia Li, Guangming Tan, Mingyu Chen, and Ninghui Sun. 2013. SMAT: An Input Adaptive Auto-Tuner for Sparse Matrix-Vector Multiplication. In Proceedings of the 34th ACM SIGPLAN Conference on Programming Language Design and Implementation (Seattle, Washington, USA) (PLDI’13). Association for Computing Machinery, New York, NY, USA, 117–126. https://doi.org/10.1145/2491956.2462181
[24] Weifeng Liu and Brian Vinter. 2015. CSR5: An Efficient Storage Format for Cross-Platform Sparse Matrix-Vector Multiplication. In Proceedings of the 29th ACM on International Conference on Supercomputing (Newport Beach, California, USA) (ICS ’15). ACM, New York, NY, USA, 339–350. https://doi.org/10.1145/2751205.2751209
[25] Xing Liu, Mikhail Smelyanskiy, Edmond Chow, and Pradeep Dubey. 2013. Efficient Sparse Matrix-vector Multiplication on x86-based Many-core Processors. In Proceedings of the 27th International ACM Conference on International Conference on Supercomputing (Eugene, Oregon, USA) (ICS ’13). ACM, New York, NY, USA, 273–282. https://doi.org/10.1145/2464996.2465013
[26] Ke Meng, Jiajia Li, Guangming Tan, and Ninghui Sun. 2019. A Pattern Based Algorithmic Autotuner for Graph Processing on GPUs. In Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming (Washington, District of Columbia) (PPoPP ’19). Association for Computing Machinery, New York, NY, USA, 201–213. https://doi.org/10.1145/3293883.3295716
[27] Robert Meusel, Sebastiano Vigna, Oliver Lehmberg, and Christian Bizer. 2014. Graph Structure in the Web — Revisited: A Trick of the Heavy Tail. In Proceedings of the 23rd International Conference on World Wide Web (Seoul, Korea) (WWW’14 Companion). ACM, New York, NY, USA, 427–432. https://doi.org/10.1145/2567948.2576928
[28] Alexander Monakov, Anton Lokhmotov, and Arutyun Avetisyan. 2010. Automatically Tuning Sparse Matrix-Vector Multiplication for GPU Architectures. In High Performance Embedded Architectures and Compilers, Yale N. Patt, Pierfrancesco Foglia, Evelyn Duesterwald, Paolo Faraboschi, and Xavier Martorell (Eds.). Springer Berlin Heidelberg, Berlin, Heidelberg, 111–125.
[29] Richard C Murphy, Kyle B Wheeler, Brian W Barrett, and James A Ang. 2010. Introducing the Graph 500. Cray Users Group (CUG) 19 (2010), 45–74.
[30] Naser Sedaghati, Te Mu, Louis-Noel Pouchet, Srinivasan Parthasarathy, and P. Sadayappan. 2015. Automatic Selection of Sparse Matrix Representation on GPUs. In Proceedings of the 29th ACM on International Conference on Supercomputing (Newport Beach, California, USA) (ICS ’15). Association for Computing Machinery, New York, NY, USA, 99–108. https://doi.org/10.1145/2751205.2751244
[31] Michelle Mills Strout, Alan LaMielle, Larry Carter, Jeanne Ferrante, Barbara Kreaseck, and Catherine Olschanowsky. 2016. An Approach for Code Generation in the Sparse Polyhedral Framework. Parallel Comput. 53, C (April 2016), 32–57. https://doi.org/10.1016/j.parco.2016.02.004

[32] W. T. Tang, R. Zhao, M. Lu, Y. Liang, H. P. Huyng, X. Li, and R. S. M. Goh. 2015. Optimizing and auto-tuning scale-free sparse matrix-vector multiplication on Intel Xeon Phi. In 2015 IEEE/ACM International Symposium on Code Generation and Optimization (CGO). 136–145. https://doi.org/10.1109/CGO.2015.7054194
[33] Anand Venkat, Manu Shantharam, Mary Hall, and Michelle Mills Strout. 2014. Non-Affine Extensions to Polyhedral Code Generation. In Proceedings of Annual IEEE/ACM International Symposium on Code Generation and Optimization (Orlando, FL, USA) (CGO’14). Association for Computing Machinery, New York, NY, USA, 185–194. https://doi.org/10.1145/2544137.2544141
[34] R. Vuduc, J. W. Demmel, K. A. Yelick, S. Kamil, R. Nishtala, and B. Lee. 2002. Performance Optimizations and Bounds for Sparse Matrix-Vector Multiply. In SC ’02: Proceedings of the 2002 ACM/IEEE Conference on Supercomputing. 26–26. https://doi.org/10.1109/SC.2002.10025
[35] Hao Wang, Liang Geng, Rubao Lee, Kaixi Hou, Yanfeng Zhang, and Xiaodong Zhang. 2019. SEP-Graph: Finding Shortest Execution Paths for Graph Processing under a Hybrid Framework on GPU. In Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming (Washington, District of Columbia) (PPoPP ’19). Association for Computing Machinery, New York, NY, USA, 38–52. https://doi.org/10.1145/3293883.3295733
[36] L. Wang, J. Zhan, C. Luo, Y. Zhu, Q. Yang, Y. He, W. Gao, Z. Jia, Y. Shi, S. Zhang, C. Zheng, G. Lu, K. Zhan, X. Li, and B. Qiu. 2014. BigDataBench: A big data benchmark suite from internet services. In 2014 IEEE 20th International Symposium on High Performance Computer Architecture (HPCA). 488–499. https://doi.org/10.1109/HPCA.2014.6835958
[37] HaoWei, Jeffrey Xu Yu, Can Lu, and Xuemin Lin. 2016. Speedup Graph Processing by Graph Ordering. In Proceedings of the 2016 International Conference on Management of Data (San Francisco, California, USA) (SIGMOD ’16). ACM, New York, NY, USA, 1813–1828. https://doi.org/10.1145/2882903.2915220
[38] Biwei Xie, Jianfeng Zhan, Xu Liu, Wanling Gao, Zhen Jia, Xiwen He, and Lixin Zhang. 2018. CVR: Efficient Vectorization of SpMV on x86 Processors. In Proceedings of the 2018 International Symposium on Code Generation and Optimization (Vienna, Austria) (CGO 2018). ACM, New York, NY, USA, 149–162. https://doi.org/10.1145/3168818
[39] Zhen Xie, Guangming Tan, Weifeng Liu, and Ninghui Sun. 2019. IA-SpGEMM: An Input-Aware Auto-Tuning Framework for Parallel Sparse Matrix-Matrix Multiplication. In Proceedings of the ACM International Conference on Supercomputing (Phoenix, Arizona) (ICS ’19). Association for Computing Machinery, New York, NY, USA, 94–105. https://doi.org/10.1145/3330345.3330354
[40] Serif Yesil, Azin Heidarshenas, Adam Morrison, and Josep Torrellas. 2020. Speeding Up SpMV for Power-Law Graph Analytics by Enhancing Locality and Vectorization. In SC20: International Conference for High Performance Computing, Networking, Storage and Analysis. https://doi.org/10.1109/SC41405.2020.00090
[41] Buse Yilmaz, Bariş Aktemur, María J. Garzarán, SamKamin, and Furkan Kiraç. 2016. Autotuning Runtime Specialization for Sparse Matrix-Vector Multiplication. ACMTrans. Archit. Code Optim. 13, 1, Article 5 (March 2016), 26 pages. https://doi.org/10.1145/2851500
[42] Y. Zhang, V. Kiriansky, C. Mendis, S. Amarasinghe, and M. Zaharia. 2017. Making caches work for graph analytics. In 2017 IEEE International Conference on Big Data (Big Data). 293–302. https://doi.org/10.1109/BigData.2017.8257937
[43] Yue Zhao, Jiajia Li, Chunhua Liao, and Xipeng Shen. 2018. Bridging the Gap between Deep Learning and Sparse Matrix Format Selection. In Proceedings of the 23rd ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (Vienna, Austria) (PPoPP ’18). Association for Computing Machinery, New York, NY, USA, 94–108. https://doi.org/10.1145/3178487.3178495

[44] Yue Zhao, Weijie Zhou, Xipeng Shen, and Graham Yiu. 2018. Overhead-Conscious Format Selection for SpMV-Based Applications. In 2018 IEEE International Parallel and Distributed Processing Symposium (IPDPS). 950–959. https://doi.org/10.1109/IPDPS.2018.00104
[45] Weijie Zhou, Yue Zhao, Xipeng Shen, and Wang Chen. 2020. Enabling Runtime SpMV Format Selection through an Overhead Conscious Method. IEEE Transactions on Parallel and Distributed Systems 31, 1 (2020), 80–93. https://doi.org/10.1109/TPDS.2019.2932931