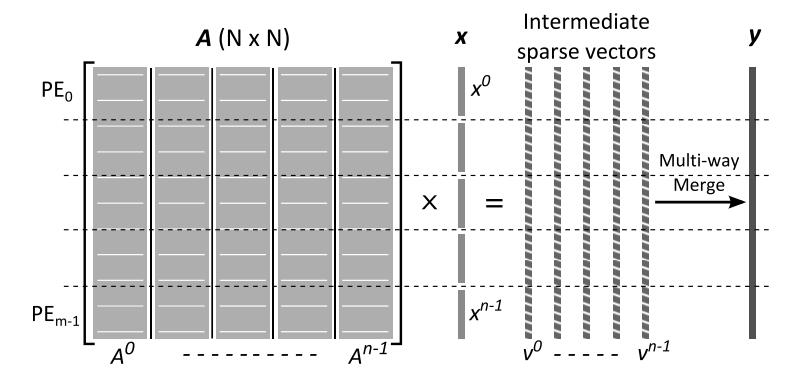
论文选读-异构平台的分布式GEMM
近期工作的Distributed-SpGEMM的相关参考太少了,考虑到本身应用的矩阵的稀疏度比较低,比较稠密,读一些分布式GEMM论文作参考。
异构平台的分布式GEMM
1 A Submatrix-Based Method for Approximate
Matrix Function Evaluation in the Quantum
Chemistry Code CP2K
本质上是对子矩阵做直接对角化,还是直接对角化方法,但是不对稠密矩阵做。
- 提出并论证了一种基于子矩阵法和矩阵符号函数的线性缩放DFT方法;
- 子矩阵方法适用于存储在分布式格式中的特定域矩阵;
- 方法在CP2K中的实现以及GPU/FPGA上的探索
Background
核心组件是DBCSR:
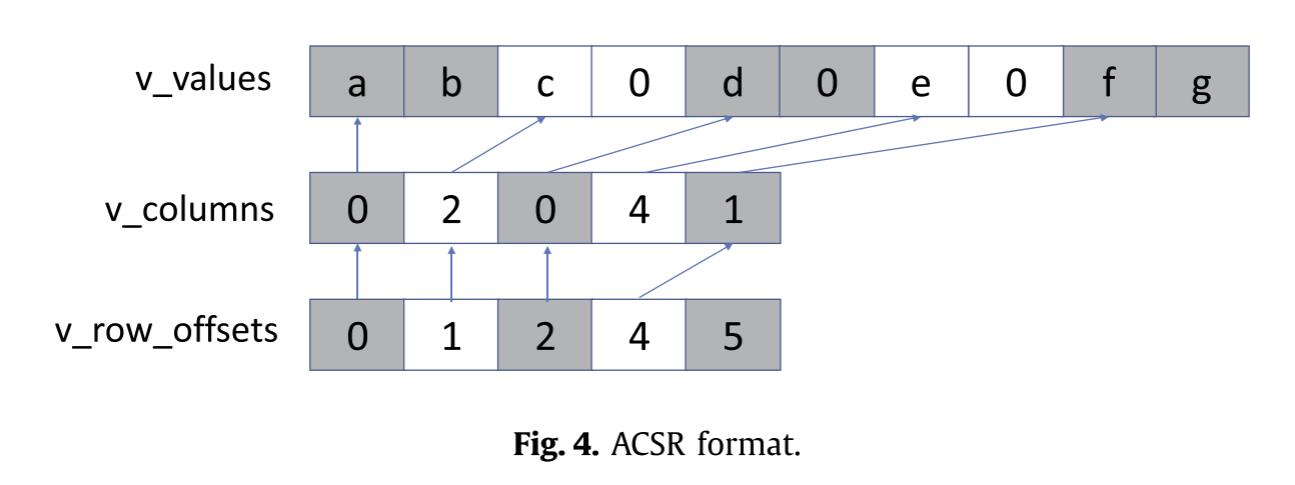
DBCSR 数据存储格式
- 矩阵被划分为 二维块网格(2D grid),每个块是一个相对较小的矩阵,通常大小为 5–30 行和列。
- 零块与非零块 的信息用 CSR(Compressed Sparse Row)格式 存储。
- 非零块 内部的数据以 密集格式(dense) 存储。
- 对于分布式处理,libDBCSR 会将 MPI 进程排列为 二维笛卡尔拓扑,并将矩阵块的行列映射到具体的 MPI rank 上,从而进行分块分配和计算。
- 矩阵乘法基于 改进的 Cannon 算法(modified Cannon’s algorithm) 实现。
- 该算法需要对许多小矩阵块进行乘法运算。
- libDBCSR 内部提供了 libsmm 库,用于小矩阵乘法的高效计算。
- 对于 Intel 系统,也可以使用 libxsmm。
- 同时,也提供了 GPU 加速版本(libsmm acc,前身为 libcusmm),进一步提升计算性能。
Sub Matrix Method
子矩阵方法是一种用于大规模稀疏对称矩阵上计算一元矩阵函数(unary matrix function)近似解的算法。它最初被提出用于求解矩阵的逆 p 次根(inverse p-th roots),后来也被应用于符号矩阵函数(sign matrix function)等场景。
非零模式(sparsity pattern)决定了矩阵中哪些元素彼此“相关”。通过对每列的局部非零邻域构建子矩阵,可以在保留主要信息的同时减少计算规模。

子矩阵方法在求解矩阵的符号函数上有一定的限制,本文推导了一个修正定义,让子矩阵方法可以用用于任意的子矩阵,从而能实现求解。
在求解DFT的时候,随着体系增大,子矩阵的尺寸在达到一定系统规模后趋于饱和。
本篇工作测试了一个液态水立方体,发现了:
- 对小体系,子矩阵会随体系增大而变大;
- 但当体系足够大(如超过约 200 个水分子),子矩阵尺寸不再增长;
- 此时计算复杂度随体系规模 线性增长(即“线性标度”)。
其数学与物理逻辑如下:
矩阵元的局域性:
由于基函数的空间局域性,矩阵元 HijH_{ij}Hij 只在距离较近的原子对之间显著。
存在有限的作用半径
对给定的基组与截断阈值,存在一个固定的最大距离,超过这个距离的原子间相互作用可以忽略
局域体积有限 → 每列的非零元有限:
因为 RmaxR_{\max}Rmax 对所有原子都是固定的,
所以每个原子(或每个基函数)只与有限个邻居产生非零矩阵元。
于是每一列/行中非零元的数目是常数,与体系规模无关。
子矩阵大小固定
总复杂度线性增长:
由于需要为每个列 iii 构建一个子矩阵并计算f(a^i)
整体计算量 ∝ 列数 n,这就是线性标度(linear scaling)的数学基础。
IMPLEMENTATION OF THE SUBMATRIX METHOD WITHIN CP2K
CP2K使用的是libDBCSR,libDBCSR的存储格式下,每个rank不知道全局的稀疏结构信息。所以实现时,所有rank把非零块以COO格式描述,然后通信让每个进程都得到全局信息。这样各个进程就能知道有哪些矩阵块需要计算,然后分配计算任务,静态分配负载,再确定需要通信的块和进程。
| 目标 | 方法 | 技术核心 | 效果 |
|---|---|---|---|
| 减少通信 | 初始化时统一数据交换 | 去重传输 | 消除重复通信 |
| 减少内存 | 相似子矩阵集中处理 | 原子排序与局域性重用 | 减少缓存大小 |
| 减少计算量 | 拆分/合并子矩阵 | 层次子矩阵或聚类合并 | 平衡 (N_S) 与 (n_i^3) |
CP2K 的子矩阵方法在并行化方面结合了分布式与共享内存两种策略。共享内存层面使用 OpenMP 实现线程级并行,主要并行化子矩阵的生成、结果提取及求解过程,这些例程均为线程安全,实现方式是通过 OpenMP 的工作共享机制将子矩阵任务分配给不同线程,从而在节点内部实现高效并行。由于不同化学环境下子矩阵规模差异较大,单纯按数量平均分配会导致负载不均,因此在分布式层面采用基于计算量估算的贪心负载均衡算法。具体地,假定每个子矩阵计算量与其维度的立方成正比,即 O(n³),程序计算各子矩阵的预期浮点操作数并依次累积分配给各 MPI rank,使每个 rank 的总计算量尽可能接近平均值,同时保证每个 rank 负责一段连续的子矩阵,以提高数据局部性并减少通信开销。这样实现的混合并行策略能够在不同层次上充分利用计算资源并保持较好的扩展性。
Evaluation
在评估子矩阵方法时,研究者在 CP2K 中将其用于从 Kohn-Sham 矩阵计算密度矩阵,按照 Eq. (16) 固定化学势 μ,即考虑大正则系综。子矩阵采用对角化方法求解,如 Section IV-F 所述。为了进行对比,同时使用传统的二阶 Newton–Schulz 迭代法计算稀疏 DBCSR 矩阵的符号函数,在迭代过程中同样使用对称正交化以保证可比性。
2 Generic matrix multiplication for multi-GPU
accelerated distributed-memory platforms over
parsec(SUMMA)
SC workshop
介绍了一个基于分布式异构平台的GEMM,基于PARSEC实现。
PARSEC:Parallel Runtime Scheduling and Execution Controller。一个转为大规模异构计算平台设计的任务型运行时系统,采用的是 任务依赖图(DAG, Directed Acyclic Graph) 的并行执行模型,支持分布式多核节点+GPU的混合系统结构。
Introduction
现代顶级超级计算机的计算性能几乎完全来自多 GPU 加速器,因此任何高性能算法都必须最大化 GPU 利用率,以在分布式多 GPU 环境中实现全局效率。
SLATE是(2019)前唯一的支持分布式多GPU系统密集矩阵运算的实现。但仅限于显存可驻留整个C的情况。本篇工作则提供了一个基于外积的分布式多GPU平台的GEMM。
Design principles
算法整体采用基于块的外积算法:
- 存储格式为2D块循环布局
- 使用外积算法计算(SUMMA),对于每个Cij,k次迭代完成计算,每次A的Ai,k进行水平广播,B的Bk,j进行垂直广播,每个节点收到后就可以更新Ci,j
- 如果采用eager mode进行通信,运行时会在一开始就触发所有广播,网络会被淹没,导致无序通信和拥塞,性能会下降,因此将整个C矩阵再次划分为bxc个更大的block of tiles。
- 每个block是逻辑同步单元
- 每个节点上的需要同时保存的tile数是T = (b+c)Kt + bc,bc是当前block的C tiles,bc要选择得恰好使这些tiles能够装进节点CPU内存
- GPU上,显存小于主存,因此引入第三个参数d:
- 把K次迭代再次切分为长度为d的chunk,每个chunk的内存需求为bc+(b+c)d
- 每个chunk结束之后有一个local barrier,防止加载太多A/B数据导致GPU内存溢出
- Chunk之间有依赖关系,从而会形成任务依赖图,由运行时系统管理
- 为了进一步提高并行度与数据重用,引入lookahead机制,当前chunk在计算时,可预取未来l个chunk所需的A、B数据。
- GPU内部任务分配:按列循环进行分配
Communication
本节主要是做一些通信量分析。
| 层次 | 控制参数 | 优化目标 | 主要受限资源 |
|---|---|---|---|
| Inter-node | (b, c) | 减少跨节点通信量 | 网络带宽 |
| Intra-node | (d) | 限制 GPU 显存占用 | GPU 内存 |
| Lookahead | ℓ | 重叠通信与计算 | GPU 内存 |
| GPU 分配 | G | 平衡负载与并行性 | 任务调度 |
节点内的CPU-GPU传输需要考虑三种情况:
| Case | 适用情况 | 内存特征 | 数据加载特征 | 传输量构成 |
|---|---|---|---|---|
| (a) | 小规模问题 | 所有需要的 tiles 都能一次放入 GPU | A/B 仅加载一次 | A: (M_t K_t / p)B: (K_t N_t / qG)C: (M_t N_t / pqG) |
| (b) | 中等规模 | B 的所有列块((c/G))能放入显存,但 A 不行 | B 一次加载,A 多次加载(每个 block column) | A: (Y \times b d)B: (K_t c/G)C: (bc/G) |
| (c) | 大规模(一般情况) | A/B 都不能完全装入显存 | A、B 都需重复加载(每 block row/col) | A: (X \times b d)B: (Y \times c d)C: (bc/G) |
因为每个进程上又对C block做了一次划分,这导致需要重复进行一些数据传输,比如Cij已经传输了Ai和Bj,之后的某个Cij+x,又需要重新传输Ai。为了最大化数据重用,尽可能减小通信次数,需要在显存允许范围内尽可能选最大的b和c,以及参数d。增加了两种子情形:
| 情形 | 特征 | 含义 |
|---|---|---|
| (c1) | 整个 (C) 可放进 GPU 显存 | 每个 GPU 只需循环加载 A/B,C 固定驻留 |
| (c2) | 整个 (C) 太大需分块 | GPU 显存中 C 也需更换;A/B 多次循环加载 |
最后,lookup参数可以根据经验值取1或2,这会导致额外存储tiles,所以取1或2这样的经验值就够了。
Implemention
对目标架构的适配
以 Summit 为代表的节点架构:
- 每个节点有 2 个 IBM Power9(P9)CPU;
- 6 块 NVIDIA GPU(V100);
- GPU 通过 NVLink 与两个 CPU 插槽相连;
- 两个 P9 之间通过 X-Bus 互联,带宽仅 64 GB/s;
- 而 GPU ↔ 最近 CPU 的 NVLink 带宽有 50 GB/s。
GPU与近端CPU通信很快,但跨CPU通信容易成为瓶颈。为减少跨 X-Bus 的通信负担,作者采用:每个节点运行两个进程,每个进程3块GPU:
通信局部化:
每个进程主要与本 socket 和本地 GPU 通信,
只有少量数据需跨 socket(经 X-Bus)传输;
减少内部竞争:
避免不同 GPU 的任务在系统后台自动拉取远程数据造成带宽冲突;
通信效率更高:
两个进程 ⇒ 两套通信管理线程(progress threads),
有助于充分利用网络带宽并减少通信系统中的排队延迟。
PARSEC 框架的默认机制是:
- 所有数据最初存在于主内存(RAM);
- 任务在需要时由运行时自动将数据从 RAM 上传到 GPU;
- 设备间通信不是显式控制的,而是根据依赖自动推断。
为改进性能,作者扩展了 PARSEC,实现:
GPU-to-GPU 直接通信(Device-to-Device transfer)。
- 每份数据有多个版本(副本)分布在不同设备;
- 运行时通过 metadata 跟踪这些副本;
- 当任务需要一个数据而目标 GPU 上没有副本时:
- 先在其他 GPU 上搜索;
- 若找到同版本的副本 ⇒ 直接通过 NVLink 复制;
- 否则再从主机内存上传。
- 引用计数与缓存管理:
- 每次 GPU 使用数据,增加引用计数;
- 当任务完成后再减少;
- 使用 LRU 策略释放显存,防止冗余副本长期占用。
编程语言的适配
PARSEC 默认是机会式调度(opportunistic scheduling):
- 所有 GPU 管理线程都可“偷取任务”(work stealing);
- 导致同一数据块可能被不同 GPU 交替计算;
- 从而造成频繁的数据迁移。
作者修改了 PARSEC 的 GPU 调度策略,利用其“last-writer heuristic”(最近写者优先)特性:
- 若某块数据最近在某 GPU 上被读写,
- 则直到该数据被显式回写到 RAM 前,
- 只有该 GPU 能继续执行涉及该数据的写操作。
在此基础上,论文新增了语言扩展:
允许用户显式指定某块数据的目标 GPU。
实现方式:
- 修改 GEMM 实现,使每块 C tile 的更新链在固定 GPU 上执行;
- 同一 tile 的所有后续更新任务都在该 GPU 上连续完成;
- 避免中途数据迁移,提高缓存复用。
Evaluation
- 机器:Summit 超级计算机(美国橡树岭国家实验室 ORNL)
- 节点构成:
- 每节点包含 2×IBM POWER9 CPU (22 cores each, 共42核心可用)
- 6×NVIDIA V100 GPU
- CPU-GPU 间通过 NVLink 2.0 互连,每个 NVLink 25 GB/s 单向带宽,总计 100 GB/s 双向带宽
- 软件栈:
- 编译器:XLC 16.1.1-2
- CUDA 9.2.148
- Spectrum MPI 10.3.0.0
- BLAS 库:cuBLAS(CUDA 自带版本)
- 运行时系统:PaRSEC + PTG (Parameterized Task Graph)
- 测试对象:并行双精度矩阵乘 PDGEMM
- 测试流程:
- 所有矩阵数据最初放在主内存(CPU RAM)
- 运行时系统负责将数据传入 GPU,执行计算
- 最终结果矩阵 C 必须写回主内存后计时结束
性能基准:
单个 V100 的实测峰值性能为 7.2 TFLOP/s(通过重复执行大矩阵 GEMM 得到)
每次实验重复 5–10 次,结果用 Tukey box plot(箱线图)展示;波动极小。
单节点实验:
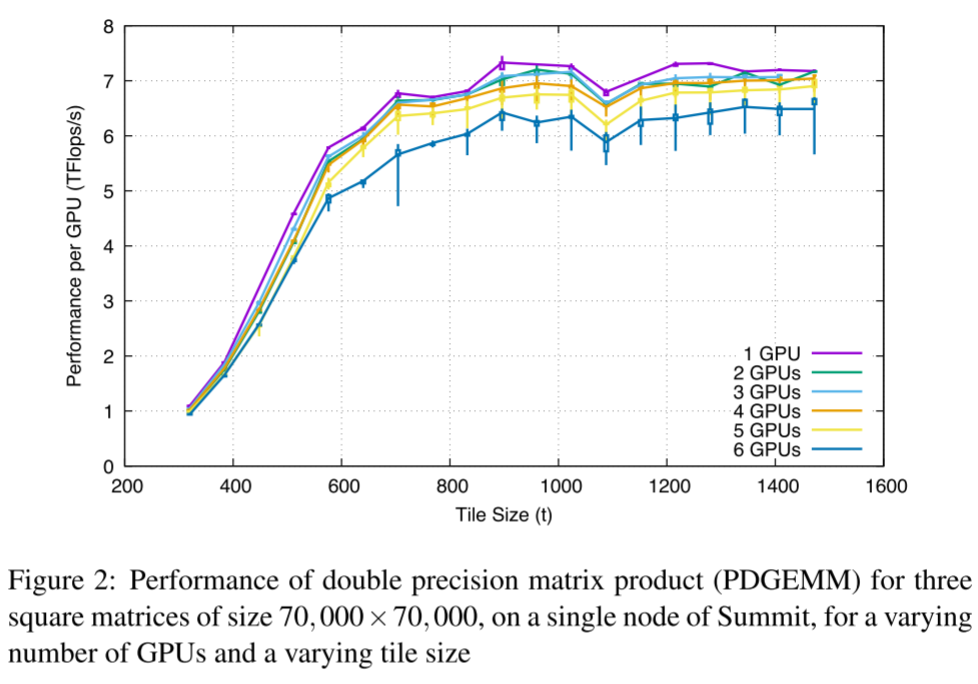
- 当 t < 1024 时,性能受 内存传输带宽 限制;
- 当 t ≥ 1024 时,算术强度足够高,达到性能 平台区(plateau);
- 单卡至三卡时性能接近峰值(>95%),四到六卡略降(≈85%),原因:
- NUMA 跨 CPU-GPU 通信带宽受限;
- X-bus 拥塞造成性能波动。
- 最终选取 t = 1024 作为后续实验的 tile 大小。
多节点实验:
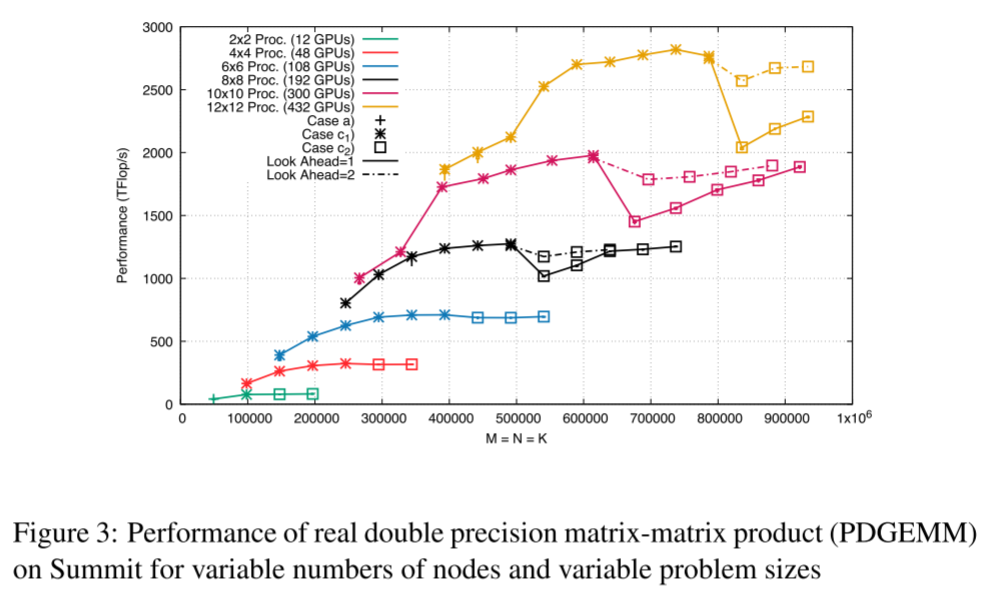
通信实验
- 实测通信量包括:
- H2D(Host→Device)
- D2H(Device→Host)
- D2D(Device↔Device)
结果:
- 实际加载的 tile 数约为模型预测的 95%(缓存复用略提升效率)
约50% 的数据加载来自 GPU 间 D2D 通信,非主存;
→ 表明 GPU 之间可共享数据块,显著减轻内存带宽压力。
PARSEC 的 LRU 缓存策略 有效减少了重复加载,提高显存利用率。