Algorithm and hardware co optimized solution for large SpMV problems

本篇论文用了特定硬件来结合优化，所以泛用性不高。但是提醒了我按行访问数据和按列访问数据，对于不同稀疏模式的矩阵来说是不一样的，另外就是尽量让x停留在缓存当中。

Abstract

SpMV 在商用 (COTS) 架构上的性能和效率很差，特别是当数据大小超过片上内存或末级缓存 (LLC) 时。这项工作提出了一种针对大型SpMV问题的算法协同优化硬件加速器。首先探讨各种 SpMV 算法的数据传输特性的基本差异。作者提出了一种算法，该算法需要最少的数据传输量，同时确保所有访问的主内存流。然而，所提出的算法需要高效的多路合并，而这在 COTS 架构中很难实现。因此，作者提出了一种硬件加速器模型，其中包括用于多路合并操作的专用集成电路（ASIC）。所提出的加速器采用了最先进的 3D 堆叠高带宽内存 (HBM)，以展示所提出的算法与最新技术相结合的能力。使用标准基准的仿真结果显示，与具有商业库的 COTS 架构相比，能源效率和性能提高了 100 倍以上。

1 Introduction

SpMV的重要性这里不在赘述。COTS 架构（CPU、GPU 等）的SpMV性能不佳的原因有两个。首先是内存墙问题，也就是说，相对于可用的计算能力，主存带宽已经很稀缺。第二，可能也是更重要的原因是，COTS 架构建立在传统的内存层次结构之上，该层次结构期望数据具有空间和时间局部性。然而，由于稀疏性，大型 SpMV 问题几乎缺乏空间和时间局部性。这使得 COTS 平台中的传统内存层次结构本质上不适合 SpMV。当我们为 SpMV 实现选择 COTS 平台时，我们会遇到架构问题。

尽管如此，研究人员研究了架构限制，并尝试通过多种技术将 SpMV 适合 COTS 架构。以CPU为例，研究人员尝试通过采用复杂的存储格式，或使用密集的预处理方法（例如寄存器分块、矩阵）来减轻矩阵结构稀疏性的影响。重新排序。对于 GPU，研究人员探索了许多复杂的方法，例如细粒度并行分解、基于模型的自动调整以及矩阵表示转换和平铺以增加时间局部性。然而，通过这些方法获得的性能和效率仍然远未达到密集矩阵运算所实现的水平。

Contributions

在这项工作中，作者提出了一种针对大型 SpMV 问题的解决方案，该解决方案在性能和效率方面比传统架构提高了 100 倍。该解决方案的关键步骤如下。

为了解决架构问题，我们从相反的方向考虑SpMV。即首先选择最适合大型 SpMV 数据传输特性的算法，然后构建所需的实现平台。作者提出了一种称为“TwoStep”的算法，该算法可确保所有数据访问的 DRAM 流式传输（即充分利用内存带宽），并消除 COTS 架构上 SpMV 实现通常所需的过多数据传输。然而，为了使该算法实现高性能和高效率，我们需要对大量长排序列表进行多路合并操作。由于使用 CPU 或 GPU 很难有效地实现这一点，因此我们提出了专用集成电路（ASIC）作为所提出的两步算法的计算平台。

为了解决内存墙问题，作者考虑最先进的 3D 堆叠主内存，即高带宽内存(HBM)和中介层技术。 HBM 提供的极限带宽显着缓解了内存墙问题。因此，我们提出了一种 SpMV 加速器模型，该模型通过中介层将TwoStep算法的 ASIC 集成到 HBM。

2 PROPOSED ALGORITHM

TwoStep算法将向量分为多段，将矩阵按列划分，存储格式为CSR。x的宽度对应于片上存储的大小，为了便于并行性化，进一步将矩阵条水平划分为块。

Step1

一个向量段从主存传输到片上存储，相应的矩阵条带也从主存读取。然后进行矩阵向量乘。每个处理元件(PE)负责为其分配的矩阵条带部分处理，所有PE共享向量段。该过程完成后，得到第k个矩阵条带的对应向量vk，PE将vk存入主存。该中间向量是稀疏的，因此位置索引与值一起存储。当我们在条带内按行方向遍历矩阵元素时，vk 的元素按照矩阵元素的行指针的升序顺序生成。因此，每个稀疏中间向量根据其元素索引（键）进行排序，这对于该算法的第二步至关重要。第一步，我们对所有矩阵条带继续此过程，最终得到 DRAM 中的 n 个稀疏中间向量。

Step2

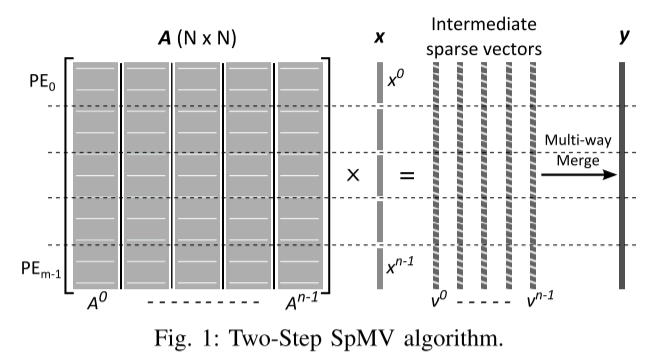
在第二步中，所有中间向量 (vks) 从主存储器流回 PE，其中本质上对这些排序列表 (vks) 进行多路合并操作以构造结果向量 y。每个PE仅合并中间向量的一部分，如图1所示。

两步算法的主要贡献在于它保证了完整的 DRAM 流式访问，同时消除了由于矩阵划分而导致的过多向量数据传输。源向量的每个元素仅从 DRAM 到片上存储进行一次传输，这对于传统架构上的大型 SpMV 实现来说通常是不正确的。作者将在第四节详细讨论这一点。

作者提出的两步算法理论上可以在 CPU 或 GPU 上实现。不幸的是，对于大型 SpMV 问题，两步法需要合并数千个排序列表，其中每个列表有数百万个元素，这是一项具有挑战性的任务。这种大型多路合并是受计算限制的，并且由于糟糕的扩展行为，很难使用 COTS 架构有效地完成。然而，通过定制硬件设计，可以实现大量长列表的高效且可扩展的多路合并。因此，作为一种解决方案，在这项工作中，作者开发了一个协同优化的 ASIC 硬件加速器，作为我们提出的两步算法的实现平台。

TwoStep的伪代码如下：

3 PROPOSED HARDWARE ACCELERATOR

作为两步算法的实现平台，作者在这项工作中开发了一个硬件加速器，如图 2 所示。对于主存储器，使用多个 HBM [15]。这种最先进的 3D 堆栈存储器可以提供极高的带宽（多个堆栈时约为 TB/s）。整个系统位于插入器底座上，在主存储器和计算核心之间提供宽广的高速通道。 HBM 与中介层一起显着缓解了 SpMV 等内存限制问题的内存墙问题。然而，应该注意的是，HBM 并不是两步算法必须有用的。

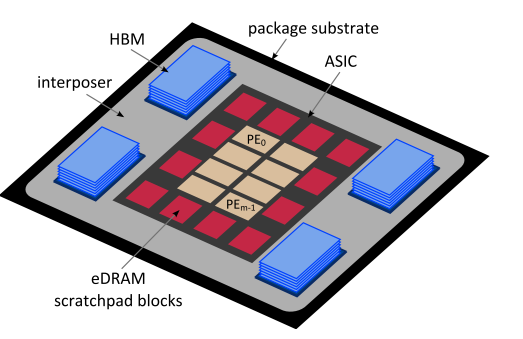
对于片上存储（算法所需的快速随机存取存储），我们使用嵌入式 DRAM (eDRAM) 暂存器。与静态随机存取存储器 (SRAM) 相比，它具有更高的密度和更低的泄漏。此外，eDRAM 使用更多的存储体和较小的页面大小，允许以适度的面积损失进行低功耗操作 [16]，并且可以提供高随机访问带宽 [17]。

PE 由两种不同类型的内核组成。第一种是乘法累加 (MA) 核心，负责算法的步骤 1。它包括多组串联的流水线浮点乘法器和加法器，如图3所示。步骤1中与矩阵条带相关的计算可以由多个PE的MA核来处理。 MA 核心总数取决于片上 eDRAM 的随机存取带宽和 DRAM 的流带宽。由于 eDRAM 具有许多小型存储体，并且访问 xk 时发生存储体冲突的可能性（由于 Ak 的稀疏性）较低，因此可以在 MA 内核之间共享片上存储，而不会在流水线中引入许多停顿。

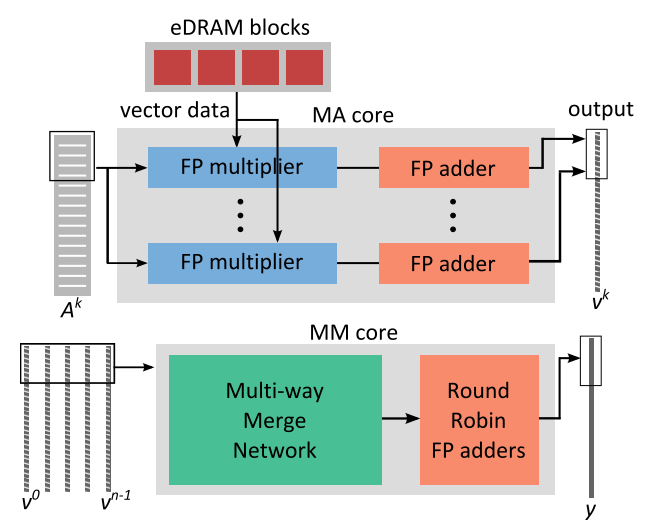
另一种类型的核心，即多路合并（MM）核心，处理第二步。基数排序网络和基于二叉树的流水线合并排序网络的组合构成了MM核心。 MM 内核的完整硬件详细信息超出了本文的范围。 MM 内核还利用 eDRAM 暂存器的一小部分来存储每个列表 (vk) 的 DRAM 页大小级别数据块。这样做是为了在每次发出列表数据的加载请求时完全摊销 DRAM 页面打开成本。定制 MM ASIC 可以提供足够高的吞吐量以使 HBM 的流带宽达到饱和。此外，多个PE的多个MM核可以并行工作并独立地合并中间向量的不同部分。

4 EVALUATION OF LARGE SPMV ALGORITHMS

SpMV 具有较高的内存访问与计算比率，因此数据传输特性是 SpMV 算法最重要的方面之一。在本节中，为了评估提出的算法，作者探讨了不同 SpMV 算法系列的数据传输特性的基本差异，同时忽略了计算要求。作者假设磁盘访问（DAM）模型建立在两级存储(主存和片上存储)之上，提出了单核场景中快速和慢速内存级别之间的数据传输的高级数学模型，但是分析也适用于多核共享内存场景。

由于高效的 SpMV 内核应该受内存限制 [1]，因此通常衡量 SpMV 算法成功与否的标准是可以实现的峰值带宽的分数。在本研究中，我们主要考虑实现完整主存（DRAM）流式访问（即利用峰值带宽）的算法。因此，我们衡量成功的标准是执行时间，它与内存层次结构级别之间传输的数据量成反比。

通常会对大型稀疏矩阵进行分区，以避免随机访问 DRAM 并实现并行化。图 4 显示了这样一个 N ×N 矩阵，该矩阵被划分为 m × n 块。使用方阵来简化计算而不失一般性。矩阵 A 总共最多有 hN 个非零值，其中 h 是每行非零值的平均数量。我们还将 Sm 定义为矩阵元素（包括元数据）的平均大小，将 Sv 定义为向量元素和结果向量元素的大小。

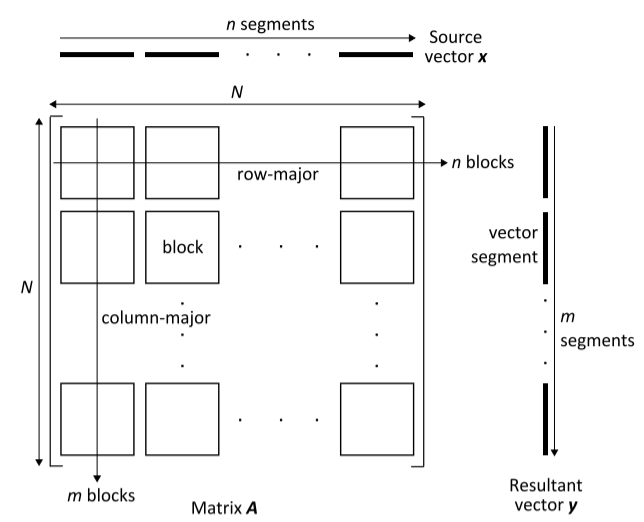
与矩阵块数据存储格式和计算方法无关，基本上有两种遍历矩阵块的方法。如图 4 所示，一种方法是按行主方向遍历块，另一种方法是按列主方向遍历块。将遵循行主块遍历的算法系列命名为 Algor，将遵循列主块遍历的其他算法命名为 Algoc。提出的 TwoStep 算法属于 Algoc 。

对于 Algor，如[19]中所使用的，源向量 (x) 的矩阵块和相关段可以从 DRAM 流式传输到芯片，并在块的乘法累加操作后被丢弃。因此，整个源向量必须从 DRAM 流式传输以遍历矩阵块的一行，并且由于尺寸较大而无法存储在芯片上以供重复使用。并且所得到的向量部分需要存储在片上以供随机访问。

因此，所得向量段 (N/m) 由片上存储大小决定。表 I 显示了 Algor 的片上存储器和 DRAM 之间的数据传输量。例如，为了计算矩阵的每个块行，需要将 hN*Sm/m 数量的矩阵数据从 DRAM 流式传输到片上存储。对于矩阵 A 的整个计算，hNSm 量的矩阵数据从 DRAM 流式传输到芯片中。从表 I 中，可以表示 Algor (Dr) 的总数据传输量，如公式 1 所示。

对于 Algoc，与 Algor 类似，矩阵块可以从 DRAM 流式传输到芯片。然而，在这种情况下，当我们沿列主方向遍历 m 个矩阵块时，需要随机访问向量 x 的段。因此，片上存储被向量段占用。与 Algor 的另一个重要区别是矩阵块的每一列都会产生一个中间结果向量。在最坏的情况下（当没有减少时），中间向量将具有与该列中所有矩阵块中的非零总数 (NNZ) 相同的元素数量。当我们移动到矩阵块的下一列时，需要更新中间结果向量。由于每次更新中间结果向量变得更加密集，因此将其存储在芯片上是不可行的。现在，我们可以通过几种方式进行更新。一种方法是将中间向量保留在 DRAM 中，并通过随机访问 DRAM 来更新其元素，但这会导致带宽使用效率低下，并使 SpMV 延迟受到限制。另一种方法是每次遍历新的矩阵块列时将整个中间结果流式传输到芯片。然而，即使保证 DRAM 流，大量冗余数据会被传输。在此方法中，必须在芯片和 DRAM 之间传输冗余数据。仅从数据传输的角度来看，更好的方法是在生成 n 个中间向量（A 的每个列块一个）时将其流式传输到 DRAM。之后，必须将所有中间向量从 DRAM 流式传输到芯片，并对它们应用归约操作以获得最终的结果向量 y。表 II 列出了 Algoc 中操作的数据传输。此外，我们可以推断出 Algoc (Dc) 的总数据传输量，如公式 2 所示。

从公式 1 和公式 2 中可以看出前两项（hNSm 和 NSv）是相同的。方程中的第三项使这些算法彼此不同。对于 Algor 来说，mNSv 的出现是因为从 DRAM 读取整个向量 m 次。另一方面，(2h+1)NSv 表示从芯片到 DRAM 往返的 Algoc 的中间结果。通过进一步研究，我们可以看到 Algor 和 Algoc 的关键因素分别是 m 和 (2h +1)。如果 m< (2h +1)，则 Algor 更可取，因为它的数据传输量比 Algoc 少。否则，当m>(2h+1)时，Algoc是优选的。

接下来，从系统配置、矩阵维度 (N) 和稀疏度 (h) 导出 m。对于任何具有 CDRAM 的 DRAM 容量的系统，给定 h，它能够处理的最大矩阵维度 N 可以通过公式 3 计算得出。假设矩阵、源向量和结果向量完全占用主存储器。

现在，Algor 需要将结果向量的第 1/m 部分存储在片上存储器中。因此，可以将片内存储器Cchip的容量表示为：

联立(3)(4)：

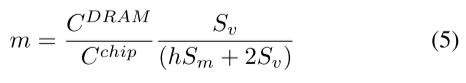
从上面的方程可以看出，m 与慢速（DRAM）和快速（片上）内存大小的比率成正比。典型系统的该比率通常远大于 SpMV 问题的矩阵稀疏度。例如，对于大型稀疏矩阵，h 可以是 1 → 10 的顺序（例如 Twitter 列表、KONECT 库中的 YouTube 等社交网络图 [20]）。另一方面，对于能够处理大型 SpMV 问题的系统，m 约为数千。

对于许多实际系统，探讨了 h = 3 时 m 的值、最大矩阵维度 N 和两种算法的执行时间（假设数据以峰值带宽传输）。表三总结了作者的发现。对于 DRAM 尺寸相对较小的系统，m 约为数百。对于具有大 DRAM 容量的系统，m 约为数千，远大于 (2h +1) = 7。因此，Algor 需要比 Algoc 更多的数据传输，特别是对于大型 SpMV 问题。例如，具有 1.5 TB DRAM 的 Haswell 服务器可以在 23B×23B 矩阵上运行，平均每行 NNZ 为 3。如果使用 Algor，则需要将 23B 元素的源向量从 DRAM 传输到芯片 m = 4200 次（600x大于 2h+1)，而对于 Algoc，源向量仅传输一次。由于中间结果的开销，对于 Algoc 来说比传输源向量 m 次要少得多，因此使用 Algoc 将执行时间缩短了 417 倍。此外，m 与矩阵维度 N 成正比，这使得 Algor 的可扩展性不如 Algoc。因此分析表明，基于列主矩阵块遍历的 SpMV 算法（例如作者提出的两步算法）更适合大型 SpMV 问题。

另一种简单的Algon算法是按照行顺序访问矩阵，对于每个元素，取出向量中对应的xj，不将整个向量流式传输到片上存储，这种算法收到延迟限制，因为需要在DRAM中随机访问，每个向量的缓存行级数数据都会传输到数据，但由于矩阵稀疏性，几乎没有重用，因此会有大量的冗余数据传输，如图5所示，灰色部分即为冗余传输：

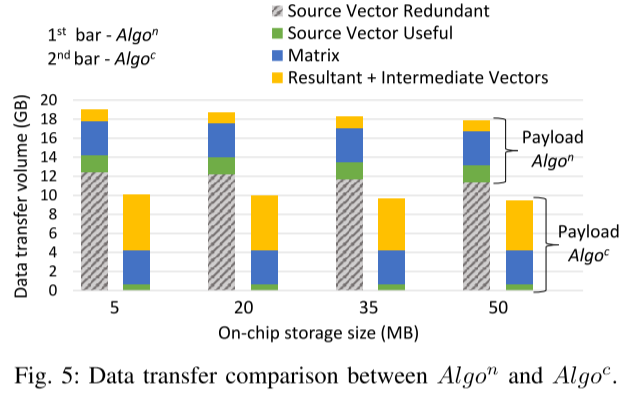
图 5 中的一个有趣的观察结果是，Algoc 的有效负载始终大于延迟限制朴素方法 (Algon)。这是因为中间向量 (vks) 必须为 Algoc 进行一次完整的往返 DRAM 的操作。尽管如此，对于迭代算法，例如PageRank [19]，通过重叠所提出算法中的两个步骤，可以消除由于 vks 往返而导致的有效负载的增加。由于篇幅有限，在本文中跳过该讨论。

5 EXPERIMENTAL RESULTS

关于硬件配置的部分跳过了。

对于测试矩阵，矩阵尺寸从 1M 到 70M 不等，每行 1 到 5 NNZ。还使用一些随机生成的稀疏矩阵来引入矩阵模式方面的最坏情况场景。作为基准测试，在双路 Xeon E5-2620 (22nm) CPU 和 Xeon Phi 5110P (22nm) 协处理器上使用 Intel Math Kernel Library (MKL) 实现了 SpMV。两种架构均具有 30MB 末级缓存 (LLC)。 CPU 峰值带宽为 102GB/s，协处理器峰值带宽为 352GB/s。此外，Nvidia CUDA Sparse (cuSPARSE) 库用于在 GTX-980 GPU 上实现 SpMV，峰值带宽为 224GB/s。能源效率和性能是针对基准进行测量的，并针对所提出的加速器进行模拟的。结果如图 6 和图 7 所示。CPU (Xeon E5) 的指标最差，而协处理器 (Xeon Phi 5110P) 的平均指标表现一般。在大多数情况下，GPU（GTX-980）在COTS架构中具有最好的效率和性能。尽管如此，所提出的加速器始终能够实现比 GPU 高两个数量级的性能和效率。这意义重大。

作者希望模拟结果能够与实际实现相匹配，因为模拟器负载假设和功率估计是悲观的。尽管如此，正确调整主存储器和 ASIC 之间的接口非常重要，以确保针对每个读写请求传输 DRAM 页大小的块数据。这对于最大限度地利用 DRAM 带宽和完全摊销 DRAM 页面打开成本至关重要。