SpV8_Pursuing_Optimal_Vectorization_and_Regular_Computation_Pattern_in_SpMV

在之前的论文阅读中，发现间隔一段时间后，即使看笔记也想不起来第一次读的完整感觉了，所以之后还是把重要的内容记在最前面。

本文作者提出了一个SpV8算法，从并行化计算的角度来优化SpMV，而矩阵格式则仍然采用CSR。这样做的原因是其他矩阵格式实现高向量利用率的同时，引入了大量的分支预测和控制代价，因此作者尝试在基本的结构上提高向量利用率，避免复杂的计算过程，从而实现高效的优化。

SpMV有两种SIMD并行策略，行内并行，跨行并行(列内的元素用一个向量寄存器计算)，作者的优化就是基于这两种策略的。行内并行对于比较长的行有效，而跨行并行对行长度相似的情况比较有效，这样的话无论行的长短，都能提高向量化率。作者的优化就是将行按长度排序，然后将长度相同的放在一起跨行并行，长度不同的行内并行，从而在避免SpMV过程复杂化的同时提高向量化率。并且为了减少排序的开销，将矩阵进行分区，对分区规模进行不同的设定。而在分区时，每8行一个单元放入分区，从而避免伪共享。

整体而言，提高SpMV的最常见的两个切入点就是提高向量化率和提高访存速度，本篇的重点是通过行内并行和跨行并行混合来提高向量化率，但不引入过多的额外执行开销，避免复杂的执行过程和规约，在访存方面没有涉及。

1 Introduction

作者首先阐述了SpMV算法的一些基本内容，并提到SpMV通常是对同一矩阵迭代进行的，因此可以对矩阵结构进行优化，因为预处理成本可以在接下来的迭代中摊销[3]。

许多研究是从格式和复杂的且不规则的计算模式来优化。本文作者认为不规则的计算会带来沉重的开销，在作者之前的研究[4]中，发现MKL由于不规则的计算流程，40%的周期会浪费在错误的分支预测上，具体来说，不规则的SpMV会遇到以下问题：

• 预测：复杂的执行流程会导致更多分支和错误预测乘法。
• 规约：最终结果的计算和顺序取决于矩阵的结构，可能需要进行规约。这会带来加法树和原子加法，损害整体性能。
• 掩码：向量操作需要掩码。不规则的计算需要设置精细的掩码来完成计算，这会带来额外的控制开销，并减少向量化的使用。

为了研究这些问题，作者分析了最先进的一些SpMV方法：CVR，CSR5，ESB。CVR和CSR5可以通过连接和扭曲行与SIMD宽度对齐来实现高度向量化。作为代价，这两种方法都需要在每次向量乘法之后检查行结束条件，以便可以正确处理最终值。每行的nnz不规则，因此这会导致大量分支预测错误。同时CSR5还需要一个灵活的加法树，进行求和操作。加法树是通过掩码向量运算实现的，这会导致掩码操作和额外向量计算开销。ESB则使用改进的ELLPACK，对行进行排序，按列进行向量计算，需要用掩码来选择列和元素，会导致额外的控制逻辑，同时，行长度的高方差也是一个问题，因为最长的行可能阻碍向量化。这让ESB对矩阵结构敏感，ESB采用列分段减轻这种影响，但是这又增加了规约的成本，需要在最后计算和总结多个列分段的部分和。

作者在XEON CPU评估上述方法，使用suitsparse中的soc-sign-epinions矩阵，这是一个社交网络矩阵，行非常稀疏，行方差很高。图2a展现了该矩阵的nnz分布。baseline是MKL的SpMV，MKL_opt是MKL的优化方法。所有的性能结果列在图2b。而图2c展现了向量使用率，图2d则展现了分支预测开销。作者将执行过程分为四类指令类型：

• SIMD Arith
• SIMD Other(load/store，permute/shuffle等)
• Scalar Arith
• Scalar Other

图2e展现了这些指令的数量。

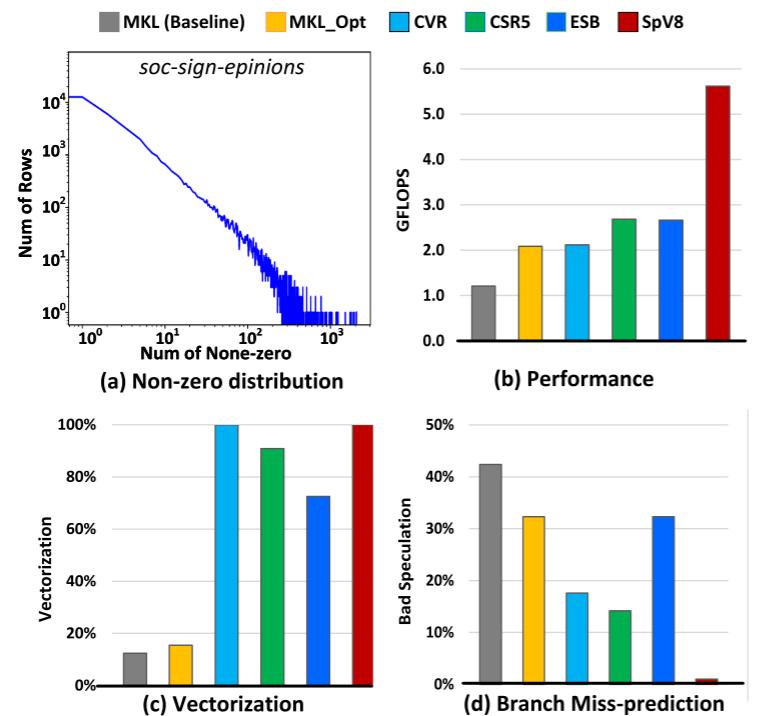
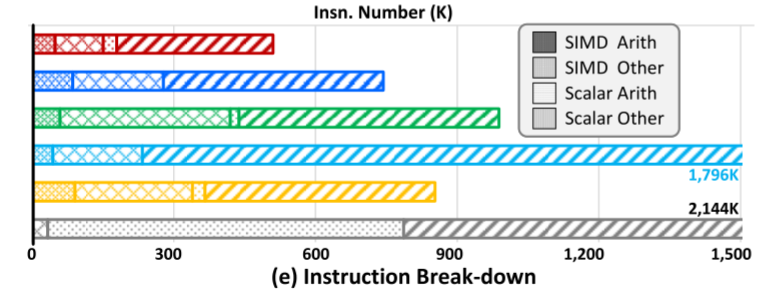
可以看到MKL的向量利用很低，而且有很高的预测开销。MKL_opt使用了更多向量指令，但是还是使用率很低。ESB提高了向量使用率，但是由于行长度的不同而带来了更多掩码操作以及多余的SIMD指令。CVR和CSR5都有很高的向量利用率，但是相应的复杂的分支带来了很大的开销。所有的结果都证实了不规则计算模式的乘法是很重的，向量使用和不规则计算模式之间的权衡是最先进的SpMV工作中的挑战。

作者提出的SpV8通过常规计算模式实现高向量化效率，在不使用复杂控制流或掩码的情况下执行最有利的计算方法。因此SpV8有显著性能优势。此外，其预处理开销也很低，表明其在许多场景有很高的适用性。

2 SpV8 Kernel Design

A. Vectorization Strategy

作者首先在 SIMD 机器上研究 SpMV 中的两种基本矢量化策略：行内并行和跨行并行，如图 3 所示。没有采用其他更复杂的策略，因为它们不可避免地会带来额外的开销，如上面各节所述。

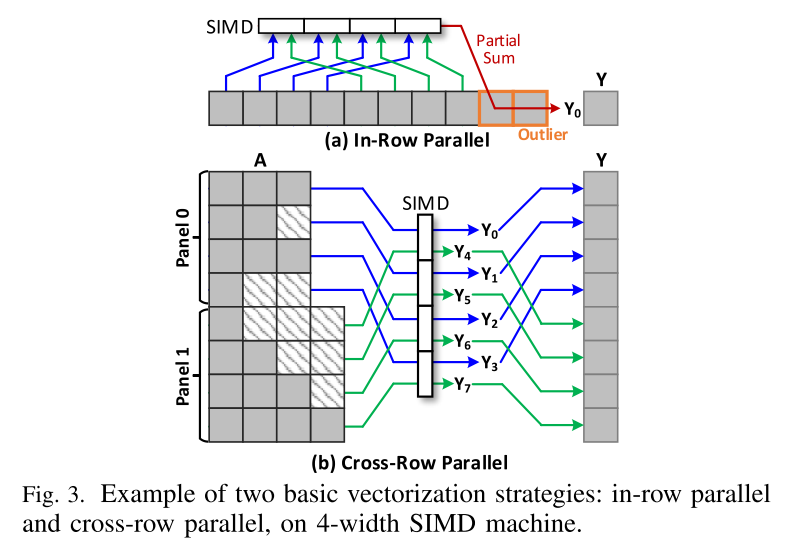
行内并行是最简单的 SIMD 实现，也是 MKL CSR SpMV 的默认算法。它收集同一行的值并在 SIMD 向量中计算它们。很明显，行内并行对于允许更高向量化使用的长行更有效。然而，对于大多数非零值位于短行中的无标度矩阵，此策略可能会遇到并行度极低的问题。

另一种基本策略是跨行并行，它使用 SIMD 通道同时处理多个panel，如图 3(b) 所示。同一panel中的行一起处理，直到计算出最长的行。向量位掩码用于在行不均匀的情况下过滤掉不需要的数据负载和计算。在相邻行具有相似长度的矩阵中，跨行并行比行内并行具有优势，因为它不需要长行来实现高向量使用。因此，一种有效的优化方法是将相同长度的行放在一起，这样更有利于跨行并行。然而，如果行的长度分布很宽，这种优化通常效果不佳。

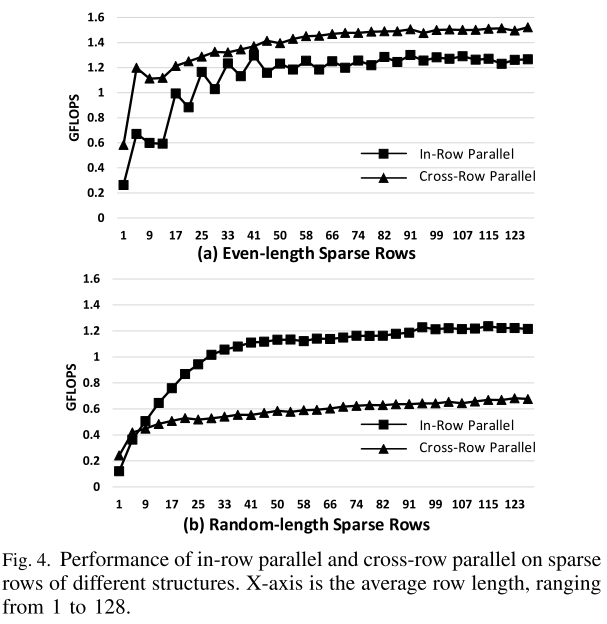
图 4 比较了两种随机生成稀疏结构的行内并行和跨行并行：等长行和随机长度行。跨行并行在等长行上实现了高性能，但在随机长度行上受到严重破坏，因为它的许多操作都被屏蔽了。从这个实验中观察到的一个有趣的现象是，行内并行的性能随着行长度的增加而迅速提高，因为较长的行可以更好地矢量化。例如，对于长度超过 40 的行，矢量化率将不低于 85%。如图 4(a) 所示，当行数为 40 或更长时，行内并行性能良好，与跨行并行相比效率更高，而跨行并行在偶数行上应该是最佳的。这表明，在长行上，行内并行是一种有效的方法，可以提供接近最佳的性能。

B. Basic Kernel

SpV8尽可能的实现接近100%的向量化，并最小化算法的复杂性，不使用部分向量操作和掩码简化计算模式。多余的nnz通过标量计算处理。并通过规则的产生结果来避免不规则的规约，从而最大限度减少条件分支的数量，图5描述了SpV8预处理步骤：

• 按行nnz的长度进行排序
• 从每个长度组的最后一行开始，将末尾的行合并到Fragment，保留向量长度行来作为Panel
• 将所有panel转为列主序格式方便计算

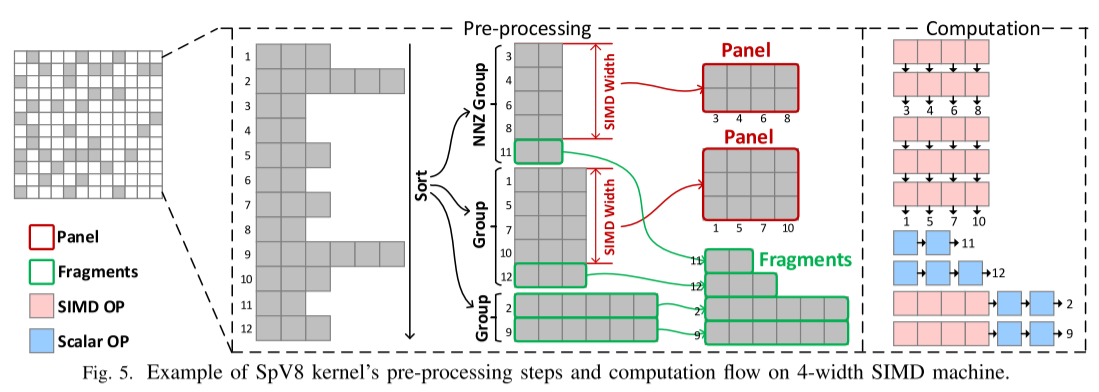
SpV8将矩阵分为Panel和一个fragment，这两部分有不同的特征。对于panel，器长度与SIMD宽度对齐，可以通过跨行并行实现最佳向量化。而fragment则更适合行内并行，而非向量化的值通过标量计算完成、这样能让SpV8的计算模式高度规则化。最终的结果也是规则产生的，不需要掩码和不规则的规约及复杂的条件分支。

C. Partitioning

SpMV的许多矩阵都是来自工业或科学场景。例如，许多社交网络矩阵都是对热链接的社交检测的结果。

社区检测：一种发现网络中紧密连接的节点群体的方法。这些群体通常代表了具有共同兴趣或行为的用户群体。通过社区检测，可以将热链接(频繁或强烈的互动)转移到对角线矩阵，这样在矩阵中，对角线附近的元素表示同一社区内的连接，反之表示不同社区之间的连接。

在材料科学问题中，nnz很可能是连续的。这种固有结构在 SpMV 中是有益的，因为它们有利于输入向量 x 上的数据重用。同时，由于输出向量y是顺序写入的，因此对y的访问也可以被忽略。

SpV8对行进行排序会改变对向量x和y的访存顺序。这可能导致局部性下降。为了避免全局排序带来对x和y访问的大量缓存缺失，矩阵被划分为多个分区，分区内进行排序。过于精细的分区会减少向量使用，产生较少的panel和更多fragment，因此分区大小的选择是访存和向量化效率之间的trade-off。

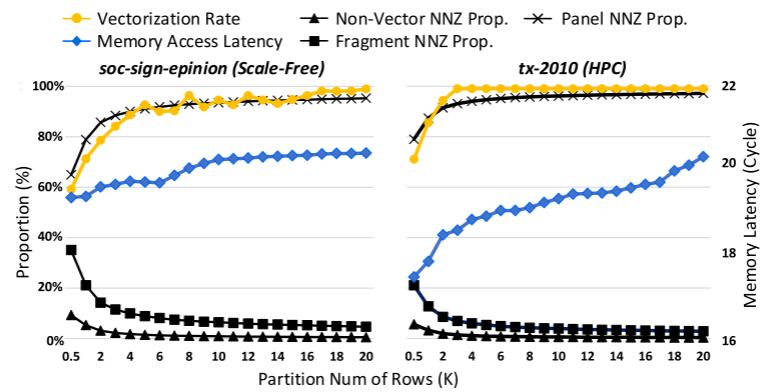
作者在两种矩阵实验了不同的分区(500-2k行)，一个是soc-sign-epinions，是一个无标度矩阵，行长度高度不规则，nnz随机分布；另一个是tx-20210，行长度限制在一个小范围，nnz分布有结构性。结果如图6。作者首先测试了panels和fragment中的nnz比例，小的分区会导致fragment很大，不过许多fragment都足够长来实现高度向量化。

因此，即使分区规模较小，SpV8 也能实现不错的矢量化率（> 90%）。另一方面，分区规模对两个矩阵的内存访问有不同的影响。 tx-2010 对规模更敏感，因为其原始位置更好，因此破坏成本更高。另一方面，分区规模的增长只会导致 soc-sign-epinions 的访存延迟轻微增加。上述观察得出的结论：不同的矩阵类型应该使用不同的权衡分区尺度，以避免大量的内存访问损失，同时仍然保持较高的向量使用率。在本文中，根据经验，无标度矩阵的分区规模设置为 10K 行左右，HPC 矩阵的分区规模设置为 2K 行左右。

3 MULTI-CORE IMPLEMENTATION

SpV8可以通过将分区给不同线程实现多核并行，为了保持平衡的工作负载，使用nnz而不是行数来创建分区，因为行的长度通常具有很高的方差。同时要求分区数量超过线程数量。虽然每个分区都是由单个线程独立计算的，但使用调度程序动态地将分区分配给空闲线程，直到处理完所有分区。这样的分区调度策略有效保证了多个线程的工作负载平衡。具体来说，每个分区的非零值阈值 Np 可以计算为：

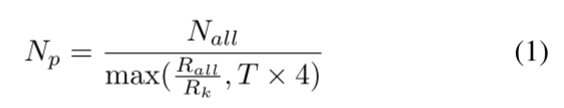
Nall是nnz，Rall是行数，T是线程数，Rk是上述提到的分区规模，通过上式保证至少4T的分区被创建。

为了避免同步或原子操作，不分割行。同时，为了避免伪共享，以Lcache/Ldata的粒度分配行，Lcache是L1缓存行大小(64byte)，Ldata是每个向量y元素的大小，以便两个线程永远不会写入同一缓存行(跨行访问，8行的元素放在一起是64byte)。在作者的实现中，使用双浮点，分配粒度为8行。所以在创建分区时，每次从矩阵中收集8行，当nnz超出Np时，当前分区就创建完成了，再创建下一个分区。

4 Evaluation

A. Experiment Setting

实验平台为Xeon Gold 6146。CPU频率限制在2.5GHz。baseline是MKL 2020.2 CSR。作者评估了ESB，CSV和CSR5的实现。所有的实现都采用AVX512。所有的方法都在单线程和8线程分别测试。benchmark是71个稀疏矩阵，36个是无标量矩阵，35个是HPC矩阵。矩阵规模从40K-2.3Billion nnz不等，行数在10K到200M之间。

B. Vectorization and Regularity

作者评估了一些无标度和 HPC 矩阵上测试方法的向量化效率。作者还通过两个指标来评估不规则计算模式的惩罚：分支推测错误（通过浪费的 µ-op 流水线的比率来衡量）和每 NNZ 指令数（通过将总指令数除以总量来计算）非零值。结果如图 7 所示。

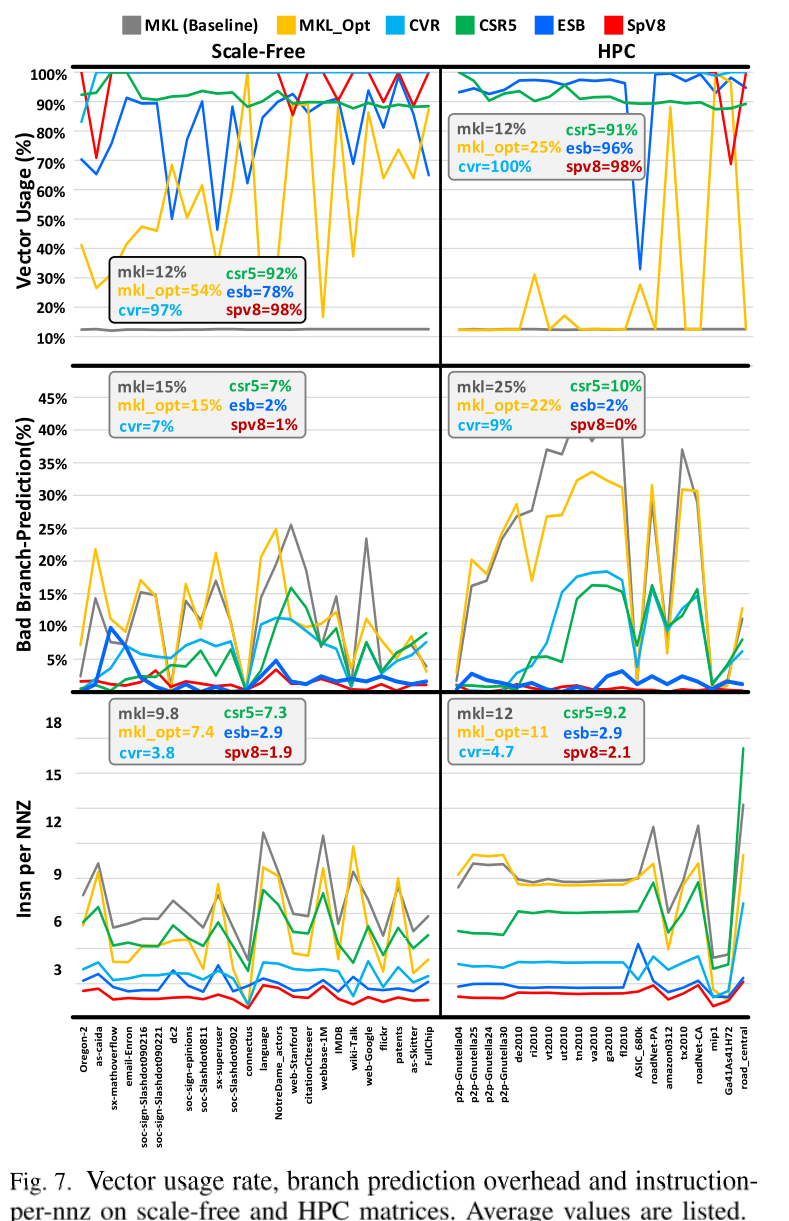
如图所示，SpV8、CVR 和 CSR5 在两种类型上均实现了较高的向量使用率。 MKL opt 更适合无标度矩阵，因为它使用行内并行，可以更好地处理不均匀的行。另一方面，ESB 使用跨行并行，这在行长度不太不规则的 HPC 矩阵上效率更高。

同时，不规则性问题对 MKL opt、CVR 和 CSR5 影响很大，因为它们往往会遇到更多的分支预测错误并需要更多的指令。有趣的是，无标度矩阵对分支预测更加友好，因为它们通常具有更可预测的很长的行。它们对 CVR 和 CSR5 也更友好，因为无标度矩阵中的长行降低了控制流和结果计算的复杂性。同时，SpV8在所有实验中表现出最小的惩罚，具有接近零的分支预测误差和最低的指令量，表明SpV8具有最小的计算复杂度。

C. Overall Performance

图 8 分别使用单线程和8线程描述了所有测试方法在无标度和 HPC 矩阵上的性能。通过tmkl/topt计算每种方法相对于 MKL 基线的加速比，其中topt和tmkl分别是优化方法和基线的运行时间。图 8 列出了所有方法的平均加速比。如图所示，在所有条件下，SpV8 都以巨大的裕度实现了最佳性能。对于所有 71 个矩阵（使用单个线程）的平均加速比，SpV8 比baseline高出 2.0 倍，比第二佳（ESB 和 CSR5）高出 1.3 倍。使用8线程时，SpV8 比基线高 2.8 倍，比第二佳 (CSR5) 高 1.4 倍。需要注意的是，对于无标度矩阵的计算，多线程kernel的实现很有挑战性，因为不规则性增加了工作负载平衡的难度，结果证明了SpV8在大规模无标度矩阵上具有良好可扩展性。

D. Pre-processing Overhead

与MKL baseline相比，SpV8的预处理时间为8x，而CVR是最小的，为6x。考虑到真实应用的潜在迭代数量，SpV8的预处理代价是可接受的。

5 Conclusion

在本文中，作者提出了 SpV8，这是一种新的 SpMV 内核，旨在在具有常规计算模式的同时实现最大向量使用。作者研究了多种计算模式在不同矩阵结构上的性能，并设计了 SpV8 以在不同的行上选择最合适的解决方案。在 Intel Xeon CPU 上的实验结果表明，SpV8 在各种矩阵类型上都优于其他最先进的方法，具有最低的复杂性和非常好的性能及很小的预处理开销。代码在https://github.com/monkey2000/spv8-public。