主页：https://hpcgame.pku.edu.cn/

赛事组的题解：https://github.com/lcpu-club/hpcgame_1st_problems

1.流量

PCAP是一种数据包记录。本题要从PCAP数据包中破解出一个密码。

破解PCAP文件的程序为/usr/bin/quantum-cracker，只能破解全部为SSH；流量的PCAP文件作为参数。

在/lustre/shared_data/potato_kingdom_univ_trad_cluster/pcaps中，有16个pcap文件，是数据包的记录，并且进行了分块。

集群的节点上有一个wireshark-cli的软件包，提供了一些命令，包括tshark和mergecap，前者可以从PCAP文件中过滤信息，后者可以合并多个PCAP文件。

本题要求使用4个计算节点，每个节点4个tshark进程同时从16个PCAP文件中提取SSH流量，要求使用Slurm调度器运行这一步骤，将这一计算的Slurm JobID和获得的密码提交。

1
2
3
4
5
6
7
8
9
#srun job
srun -pC064M0256G -N4 --ntasks-per-node=4 bash -c 'tshark -r /lustre/shared_data/potato_kingdom_univ_trad_cluster/pcaps/$SLURM_PROCID.pcap -Y ssh -w $SLURM_PROCID.ssh.pcap'

#jobID
sacct -u $(whoami) --format JobID | tail

#merge&decode
mergecap -w merged.pcap *.ssh.pcap
/usr/bin/quantum-cracker merged.pcap

2.高性能数据校验

题目提到的高性能校验算法如下：算法的流程如下（对算法的具体解释见 baseline 代码）：

  • 对数据进行分块，每一块的大小为 M=1MB，记划分的块数为 n。如果文件剩余内容不足一块的大小，则补二进制0至一个块大小。

  • 对于第 i 个块，在其末尾连接上第 i-1 个块的 SHA512 校验码的二进制值，将所得到的 M + 64 大小的数据进行 SHA512 校验，得到第 i 个块的校验码。（i 从 0 开始，第 -1 个块的校验码为空文件的校验码）

  • 最后一个块的校验码，即为文件的校验码

调用SHA512()计算和给出的代码中的计算是等价的。

baseline版本如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void checksum(uint8_t *data, size_t len, uint8_t *obuf) {
  int num_block = (len + BLOCK_SIZE - 1) / BLOCK_SIZE;
  uint8_t prev_md[SHA512_DIGEST_LENGTH];

  EVP_MD_CTX *ctx = EVP_MD_CTX_new();
  EVP_MD *sha512 = EVP_MD_fetch(nullptr, "SHA512", nullptr);

  //SHA512(data, len, md);
  SHA512(nullptr, 0, prev_md);
  for (int i = 0; i < num_block; i++) {
    uint8_t buffer[BLOCK_SIZE]{};
    EVP_DigestInit_ex(ctx, sha512, nullptr);
    std::memcpy(buffer, data + i * BLOCK_SIZE,
                std::min(BLOCK_SIZE, len - i * BLOCK_SIZE));
    EVP_DigestUpdate(ctx, buffer, BLOCK_SIZE);
    EVP_DigestUpdate(ctx, prev_md, SHA512_DIGEST_LENGTH);

    unsigned int len = 0;
    EVP_DigestFinal_ex(ctx, prev_md, &len);
  }

  std::memcpy(obuf, prev_md, SHA512_DIGEST_LENGTH);
  EVP_MD_CTX_free(ctx);
  EVP_MD_free(sha512);
}

因为可以先计算块本身的数据，最后再加上上一个块的校验码，所以可以首先并行计算每个块本身的数据(第一块除外，可以直接完整计算)，计算完毕后，接收上一个节点的计算结果，更新自己的每个块的校验码，再将最后一个块的校验码传给下一个节点。使用MPI的IO接口读入数据，因为最后一个测试点是16G文件，每个节点要读4G文件，超过了单词读入的size参数(32位整型)，所以要分两次读入。但是这个版本只能拿到74分，正解是边读边接收上一块计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
namespace fs = std::filesystem;

constexpr size_t BLOCK_SIZE = 1024 * 1024;

void print_checksum(std::ostream &os, uint8_t *md, size_t len);

int main(int argc, char *argv[]){
    MPI_Init(&argc, &argv);
    int rank, nprocs;
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &nprocs);

    auto t1 = std::chrono::steady_clock::now();
    //check arg
    if(rank==0){
        if (argc < 3) {
            std::cout << "Usage: " << argv[0] << " <input_file> <output_file>"<< std::endl;
            MPI_Abort(MPI_COMM_WORLD, 1);
        }
    }

    //read file----------------------------------------------------------------
    fs::path input_path = argv[1];
    fs::path output_path = argv[2];
    auto file_size = fs::file_size(input_path);
    std::cout << input_path << " size: " << file_size << std::endl;
    uint8_t *file_buffer = nullptr;

    int num_block = (file_size + BLOCK_SIZE - 1) / BLOCK_SIZE;
    int block_per_proc = num_block/nprocs;
    int nblocks;
    if(rank!=nprocs-1)  nblocks = block_per_proc;
    else nblocks = num_block - (nprocs-1)*block_per_proc;

    MPI_File file;
    MPI_File_open(MPI_COMM_WORLD, argv[1], MPI_MODE_RDONLY, MPI_INFO_NULL, &file);

    MPI_Offset global_offset = rank * block_per_proc * BLOCK_SIZE;
    size_t my_data_size;
    if(rank!=nprocs-1) my_data_size = nblocks*BLOCK_SIZE;
    else my_data_size = file_size - block_per_proc*BLOCK_SIZE*(nprocs-1);
    file_buffer = new uint8_t[my_data_size];
    size_t exceed_size = 1024*1024;
    exceed_size *= 1024*8;
    if(file_size<exceed_size) MPI_File_read_at(file, global_offset, file_buffer, my_data_size, MPI_BYTE, MPI_STATUS_IGNORE);
    else{
        MPI_File_read_at(file, global_offset, file_buffer, my_data_size/2, MPI_BYTE, MPI_STATUS_IGNORE);
        MPI_File_read_at(file, global_offset + my_data_size/2, file_buffer + my_data_size/2, my_data_size-my_data_size/2, MPI_BYTE, MPI_STATUS_IGNORE);
    }
    //caculation----------------------------------------------------------------
    if (rank == 0) {
        
        //caculate checksum---------------------------------------------
        uint8_t obuf[SHA512_DIGEST_LENGTH];
        
        //calculate my block
        EVP_MD_CTX *ctx = EVP_MD_CTX_new(); 
        EVP_MD *sha512 = EVP_MD_fetch(nullptr, "SHA512", nullptr);
        uint8_t prev_md[SHA512_DIGEST_LENGTH];
        SHA512(nullptr, 0, prev_md);
        for(int i=0;i<nblocks;i++){
            EVP_DigestInit_ex(ctx, sha512, nullptr);
            EVP_DigestUpdate(ctx, file_buffer + i * BLOCK_SIZE, BLOCK_SIZE);
            EVP_DigestUpdate(ctx, prev_md, SHA512_DIGEST_LENGTH);
            unsigned int len = 0;
            EVP_DigestFinal_ex(ctx, prev_md, &len);
        }
        //send my last 
        MPI_Send(prev_md, SHA512_DIGEST_LENGTH, MPI_UINT8_T, 1, 0, MPI_COMM_WORLD);
        EVP_MD_CTX_free(ctx);
        EVP_MD_free(sha512);
    }
    else{
        //caculate my block
        EVP_MD_CTX *ctx[nblocks]; 
        EVP_MD *sha512 = EVP_MD_fetch(nullptr, "SHA512", nullptr);
        if(rank!=nprocs-1){
            for(int i=0;i<nblocks;i++){
                ctx[i] = EVP_MD_CTX_new();
                EVP_DigestInit_ex(ctx[i], sha512, nullptr);
                EVP_DigestUpdate(ctx[i], file_buffer + i * BLOCK_SIZE, BLOCK_SIZE);
            }
        }
        else{
            for(int i=0;i<nblocks-1;i++){
                ctx[i] = EVP_MD_CTX_new();
                EVP_DigestInit_ex(ctx[i], sha512, nullptr);
                EVP_DigestUpdate(ctx[i], file_buffer + i * BLOCK_SIZE, BLOCK_SIZE);
            }
            size_t x = nblocks-1; 
            ctx[x] = EVP_MD_CTX_new();
            uint8_t buffer[BLOCK_SIZE]{};
            EVP_DigestInit_ex(ctx[x], sha512, nullptr);
            std::memcpy(buffer, file_buffer + x * BLOCK_SIZE, my_data_size - x * BLOCK_SIZE);
            EVP_DigestUpdate(ctx[x], buffer, BLOCK_SIZE);
        }
        //prev
        uint8_t prev_md[SHA512_DIGEST_LENGTH];
        MPI_Recv(prev_md, SHA512_DIGEST_LENGTH, MPI_UINT8_T, rank-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
        for (int i = 0; i < nblocks; i++) {
            EVP_DigestUpdate(ctx[i], prev_md, SHA512_DIGEST_LENGTH);
            unsigned int len = 0;
            EVP_DigestFinal_ex(ctx[i], prev_md, &len);
        }
        //send my last
        if(rank != nprocs-1) MPI_Send(prev_md, SHA512_DIGEST_LENGTH, MPI_UINT8_T, (rank+1)%nprocs, 0, MPI_COMM_WORLD);
        else{
            // write checksum to output file
            std::ofstream output_file(output_path);
            print_checksum(output_file, prev_md, SHA512_DIGEST_LENGTH);
        }
        for(int i=0;i<nblocks;i++){
            EVP_MD_CTX_free(ctx[i]);
        }
        EVP_MD_free(sha512);
    }

    auto t2 = std::chrono::steady_clock::now();
    int d1 = std::chrono::duration_cast<std::chrono::milliseconds>(t2 - t1).count();
    if(rank==0) printf("%dms\n", d1);

    MPI_File_close(&file);
    delete[] file_buffer;
    MPI_Finalize();

    return 0;
}

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
#include <cstdint>
#include <cstring>
#include <fcntl.h>
#include <filesystem>
#include <fstream>
#include <iostream>
#include <mpi.h>
#include <openssl/evp.h>
#include <openssl/sha.h>
#include <sys/mman.h>
#include <unistd.h>

#define DIGEST_NAME "SHA512"

namespace fs = std::filesystem;

constexpr size_t BLOCK_SIZE = 1024 * 1024;

void print_checksum(std::ostream &os, uint8_t *md, size_t len);

int get_num_block(int rank, int nprocs, int num_block_total)
{
    return num_block_total / nprocs + ((rank < num_block_total % nprocs) ? 1 : 0);
}

int main(int argc, char *argv[])
{

    MPI_Init(&argc, &argv);

    int rank, nprocs;
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    MPI_Comm_size(MPI_COMM_WORLD, &nprocs);

    int num_block_total, num_block, fd;
    size_t file_size;

    EVP_MD_CTX *ctx = EVP_MD_CTX_new();
    EVP_MD *sha512 = EVP_MD_fetch(nullptr, DIGEST_NAME, nullptr);

    fs::path input_path, output_path;
    uint8_t *file_buffer = nullptr;

    if (rank == 0)
    {
        if (argc < 3)
        {
            std::cout << "Usage: " << argv[0] << " <input_file> <output_file>"
                      << std::endl;
            MPI_Abort(MPI_COMM_WORLD, 1);
        }
    }
    input_path = argv[1];
    output_path = argv[2];
    if (rank == 0)
    {
        file_size = fs::file_size(input_path);
        std::cout << input_path << " size: " << file_size << std::endl;
    }

    MPI_Bcast(&file_size, 1, MPI_INT64_T, 0, MPI_COMM_WORLD);
    num_block_total = (file_size + BLOCK_SIZE - 1) / BLOCK_SIZE;
    num_block = get_num_block(rank, nprocs, num_block_total);

    MPI_Datatype filetype, contig;
    MPI_Offset disp;
    MPI_Type_contiguous(BLOCK_SIZE, MPI_BYTE, &contig);
    MPI_Type_create_resized(contig, 0, nprocs * BLOCK_SIZE, &filetype);
    MPI_Type_commit(&filetype);

    MPI_Offset offset = rank * BLOCK_SIZE;
    MPI_File fh;

    MPI_File_open(MPI_COMM_WORLD, input_path.c_str(), MPI_MODE_RDONLY,
                  MPI_INFO_NULL, &fh);
    MPI_File_set_view(fh, offset, MPI_BYTE, filetype, "native", MPI_INFO_NULL);

    uint8_t prevdigest[SHA512_DIGEST_LENGTH];
    uint8_t outdigest[SHA512_DIGEST_LENGTH];
    MPI_Request request[2] = {MPI_REQUEST_NULL, MPI_REQUEST_NULL};
    int nblk_index = 0;

    uint8_t curr_block[BLOCK_SIZE];
    for (int i = 0; i < num_block; i++)
    {
        MPI_File_read(fh, curr_block, BLOCK_SIZE, MPI_BYTE, MPI_STATUS_IGNORE);

        unsigned int len = 0;

        if (rank == 0 && i == 0)
        {
            SHA512(nullptr, 0, prevdigest);
        }
        else
        {
            // receive the checksum of prev data block
            MPI_Irecv(prevdigest, SHA512_DIGEST_LENGTH, MPI_BYTE,
                      (rank == 0 ? nprocs - 1 : rank - 1), 1, MPI_COMM_WORLD,
                      &request[0]);
        }

        EVP_DigestInit_ex(ctx, sha512, nullptr);

        EVP_DigestUpdate(ctx, curr_block, BLOCK_SIZE);

        MPI_Waitall(2, request, MPI_STATUSES_IGNORE);

        EVP_DigestUpdate(ctx, prevdigest, SHA512_DIGEST_LENGTH);

        EVP_DigestFinal_ex(ctx, outdigest, &len);

        if (i * nprocs + rank == num_block_total - 1)
        {
            // send the result to rank 0
            MPI_Send(outdigest, SHA512_DIGEST_LENGTH, MPI_BYTE, 0, 2, MPI_COMM_WORLD);
        }
        else
        {
            // send to checksum to the next data block
            MPI_Isend(outdigest, SHA512_DIGEST_LENGTH, MPI_BYTE, (rank + 1) % nprocs,
                      1, MPI_COMM_WORLD, &request[1]);
        }
    }

    MPI_File_close(&fh);

    if (rank == 0 && num_block == 0)
    {
        // deal with the situation that file_size is 0
        SHA512(nullptr, 0, outdigest);
        MPI_Send(outdigest, SHA512_DIGEST_LENGTH, MPI_BYTE, 0, 2, MPI_COMM_WORLD);
    }

    if (rank == 0)
    {
        // receive result
        uint8_t resultdigest[SHA512_DIGEST_LENGTH];
        MPI_Recv(resultdigest, SHA512_DIGEST_LENGTH, MPI_BYTE, MPI_ANY_SOURCE, 2,
                 MPI_COMM_WORLD, MPI_STATUS_IGNORE);

        std::ofstream output_file(output_path);
        print_checksum(output_file, resultdigest, SHA512_DIGEST_LENGTH);
    }

    EVP_MD_free(sha512);
    EVP_MD_CTX_free(ctx);

    MPI_Finalize();

    return 0;
}

void print_checksum(std::ostream &os, uint8_t *md, size_t len)
{
    for (int i = 0; i < len; i++)
    {
        os << std::setw(2) << std::setfill('0') << std::hex
           << static_cast<int>(md[i]);
    }
}

3.齐心协力(RAY)

ray是python实现的消息传递API，本题对于每个数据，需要4个步骤完成，因此可以构建四个worker组成的流水线，进行数据处理。

与上一题相同，本题也只拿了75分，两个题API不同，但过程是相似的，因此可能是有同样的可以优化的地方。

RAY的文档：https://docs.ray.io/en/latest/ray-core/walkthrough.html

最后还是看题解才知道做这个题对RAY的理解很多地方还是有问题。当时看文档没有仔细看。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
import os
import ray
import numpy as np
import time
from multiprocessing.pool import ThreadPool
from ray.util.placement_group import (
    placement_group,
    placement_group_table,
    remove_placement_group,
)
from ray.util.scheduling_strategies import PlacementGroupSchedulingStrategy

#Actor---------------------------------------------------------------------------------------------
@ray.remote(num_cpus=4)  # 指定每个worker需要4个CPU
class workerA:
    def __init__(self,rank):
        self.pool = ThreadPool(4)
        self.next = None
        self.rank = rank
        self.weight = (np.load(f"weights/weight_{rank}.npy"))

    def set_next(self,next):
        self.next = next
    
    def read_data(self, i):
        mtx = np.load(f"inputs/input_{i}.npy")
        return mtx

    def write_data(self, data_struct):
        i = data_struct[0]
        mtx = data_struct[1]
        np.save(f"outputs/output_{i}.npy", mtx)
        return True

    def process_data(self, mtx):
        mtx = np.dot(mtx, self.weight)
        mtx = np.maximum(0, mtx)
        return mtx


    # mtx是包含四个矩阵的列表
    def process(self, i, mtx = None):
        if self.rank==0:
            mtx = self.pool.map(self.read_data, range(i,i+4))
        
        #每个worker都要处理
        mtx = self.pool.map(self.process_data, mtx)
        
        #处理结果
        if self.next is None:
            data_pack = []
            for k in range(4):
                data_pack.append([i+k, mtx[k]])
            ret = self.pool.map(self.write_data, data_pack)
        else:
            return self.next.process.remote(i, mtx)

#--------------------------------------------------------------------------------------------------
ray.init(address=f"{os.environ['RAY_CLUSTER_ADDR']}",log_to_driver=True)
# 每个bundle4个CPU，4个bundle
pg = ray.util.placement_group([{"CPU": 4}] * 4, strategy="PACK")
ray.get(pg.ready())

# 创建worker
firstw = workerA.options(placement_group=pg, placement_group_bundle_index=0).remote(0)
secw = workerA.options(placement_group=pg, placement_group_bundle_index=1).remote(1)
thirdw = workerA.options(placement_group=pg, placement_group_bundle_index=2).remote(2)
lastw = workerA.options(placement_group=pg, placement_group_bundle_index=3).remote(3)
ray.get(firstw.set_next.remote(secw))
ray.get(secw.set_next.remote(thirdw))
ray.get(thirdw.set_next.remote(lastw))

if not os.path.exists("outputs"):
    os.mkdir("outputs")

# 启动流水线
refs = []
for i in range(0,100,4):
    refs.append(firstw.process.remote(i))

# get result
for i in range(25):
    ref = ray.get(refs[i])  # workB remote ref
    ref = ray.get(ref)      # workC remote ref
    ref = ray.get(ref)      # workD remoteref
    ret = ray.get(ref)

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#!/usr/bin/env python

import ray
import numpy as np
import time
import os

num_batches = 100
num_workers = 4
input_prefix = "inputs"
output_prefix = "outputs"
weight_prefix = "weights"

@ray.remote(num_cpus=4)
class Worker:

    def __init__(self, weight_path: str, rank: int):
        self.weight = np.load(weight_path)
        self.rank = rank
    
    def calculate(self, x: np.ndarray):
        return np.maximum(x @ self.weight, 0)
    
def main():
    
    start_time = time.time()

    if not os.path.exists(output_prefix):
        os.makedirs(output_prefix)
    
    feature = np.load(f"{input_prefix}/input_0.npy")
    
    workers = []
    features = []
    
    ray.init()
    
    for worker_idx in range(0, num_workers):
        workers.append(Worker.remote(f"{weight_prefix}/weight_{worker_idx}.npy", worker_idx))
    
    for input_idx in range(0, num_batches):
        for worker in workers:
            feature = worker.calculate.remote(feature)
        features.append(feature)
        if input_idx != num_batches - 1:
            feature = np.load(f"{input_prefix}/input_{input_idx + 1}.npy")
    
    for i, result in enumerate(features):
        output = ray.get(result)
        np.save(f"outputs/output_{i}.npy", output)
    
    print(f"Time taken: {time.time() - start_time}")
    
if __name__ == "__main__":
    main()

4.3D生命游戏

人工智能编程 | 谭升的博客 (face2ai.com)

CUDA编程入门极简教程 - 知乎 (zhihu.com)

本题只拿了10分，直接等题解。

5.矩阵乘法

最经典的高性能计算实例，这次终于看懂goto算法了，但是在实现的过程中实际上是写了一个简化的版本，但是pack和缓存都考虑到了，所以分数还可以，150/200。

尽管用以下一张图就可以表示这个算法，真的完全理解和实现还是更复杂一些。

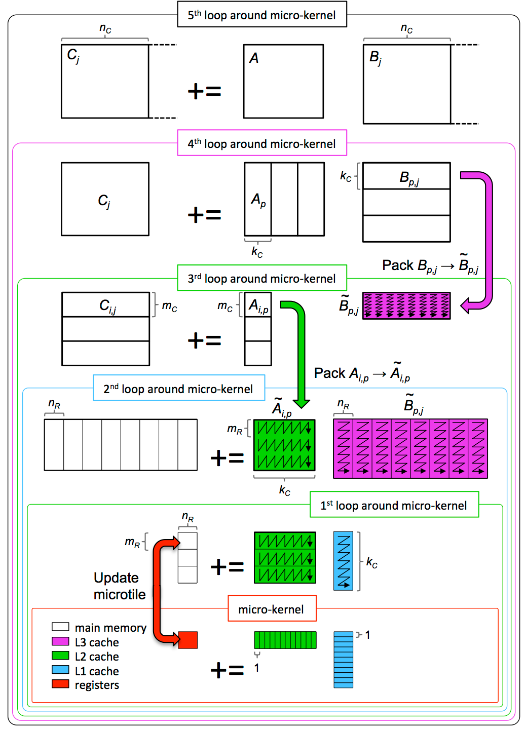
GOTO算法

计算记为C = A x B。

单独画了和上方不一样的图，是因为要提醒自己，每个块划分完之后是存在偏移的，数据定位是要考虑偏移的。一直到第二层循环，数据都打包好了以后，就可以将原问题转为子矩阵和子矩阵的计算了。

对于大型矩阵乘法计算，由于数据规模大，局部性会变得非常差。为了提高局部性，要对矩阵进行分块，对矩阵分块有多种分块计算方式。如果矩阵比较小，可以直接将矩阵C横向和纵向都进行划分，分为小块进行计算，也就是6重循环的计算方法，但是如果矩阵规模大，这种方式就会因为没有很好的利用到局部性而性能快速下降。所以对于大规模的矩阵，要一步一步划分，考虑每个划分后的子矩阵的计算方式，来最大化局部性。在goto算法中，主要利用到的是以下这两种划分方式，一个是按列，一个是分层。

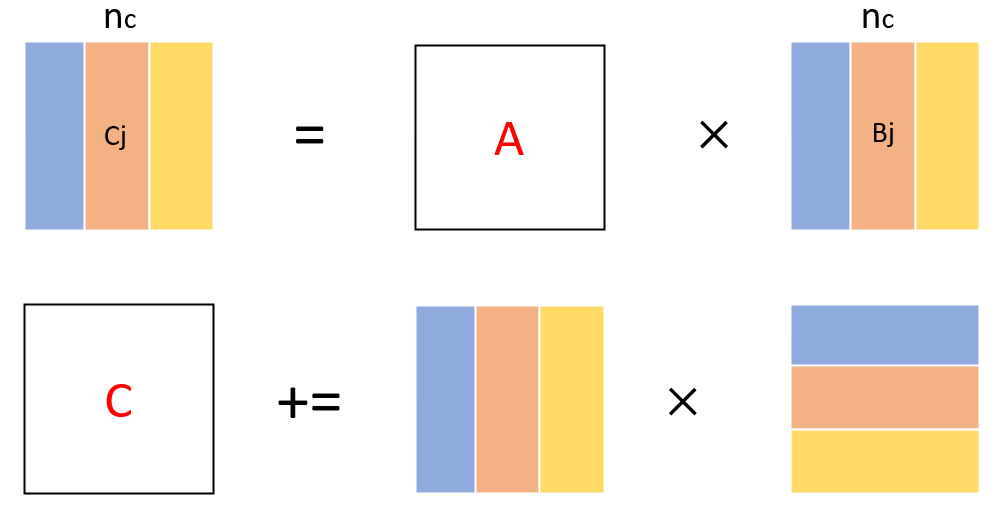
image-20240205210352046

首先通过按列划分，减少矩阵计算的规模，每次计算Cj，Cj包含nc列，Cj的起始列号假设为js，此后访问Cj和Bj的数据都要注意加上js这个偏移量。此时C(i，j)为C[ldc*i + j + js]，矩阵按行存储。

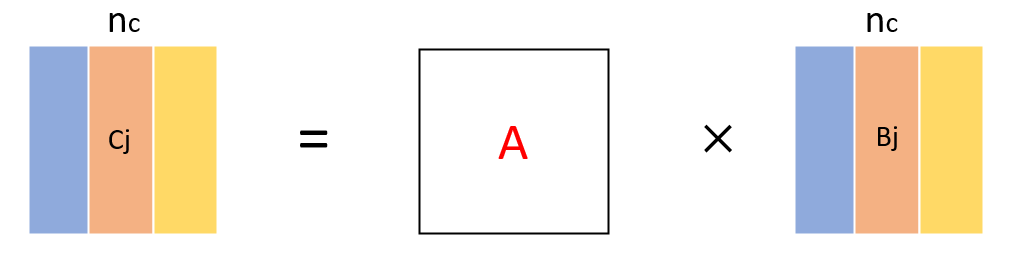
image-20240205210415849

而对于Cj的计算，按照分层的方式进行划分：

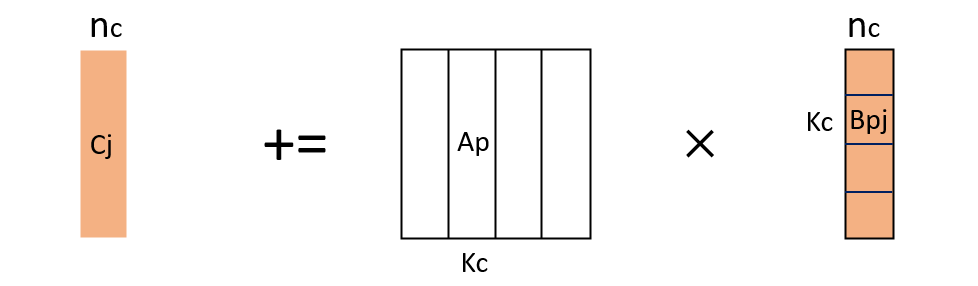
image-20240205210839211

此时的Bpj已经经过两次划分，可以对其进行打包，至于打包的格式，取决于最核心kernel对其的计算方式，这里可以先不看。打包的目的是为了加快计算和提升局部性，接下来还要对Cj进行划分，这次按照行进行划分，子矩阵的计算就变成了Aip和Bpj的计算，Bpj会在计算Cij时反复使用，因此可以考虑将其大小与L3Cache适配。这里打包时，假设起始行号为as，将as行起的kc行打包到单独的一块内存。

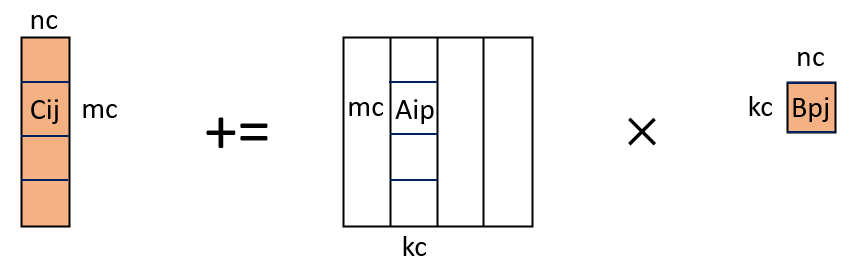
image-20240205211152664

到了这里，计算已经划分为Cij += Aip × Bpj，可以将其作为一个macro kernel封装了。而A也已经划分为一个块，可以将其打包，以便于计算和放入缓存，此时L3已经存入Bpj，Aip作为更小的块，将其适配L2缓存。而对于每一个Cij，在内部再进行划分，此时Aip和Bpj都是打包后的了，可以不考虑原矩阵中的位置而访问数据，只有C的数据访问还需要在原矩阵中定位。Cij内部的划分和上述过程是一样的，先按列划分，再按行划分，最后计算子矩阵块，这时就可以直接搬出这个图了：

按照最终的计算顺序，对A和B进行相应的打包来加快计算。在我的实现中，最内层的kernel不是分层划分计算的，而是按照常规的矩阵乘法应用AVX计算的。

实现

这里假定大小是可以对齐，多加上长度的控制，就可以对通用大小进行计算了。此外，macro_kernel也不是严格按照上述算法分解的，但是原理是一致的，划分大小也是按照packB在L3缓存，packA在K2缓存，最小计算在L1和向量寄存器中完成而设定的。

gemm的整体实现如下，为了多线程并行计算，准备线程数个packA的打包缓冲区，在第三层循环这里进行多线程并行计算，注意macro_kernel传入的packA地址是当前线程对应的packA地址。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
const uint64_t gemm_nc = 4096;
const uint64_t gemm_kc = 1024;
const uint64_t gemm_mc = 64;
const uint64_t gemm_mr = 8;
const uint64_t gemm_nr = 32;
const int ncore = omp_get_num_procs();

void mul_opt(double* a, double* b, double* c, uint64_t n1, uint64_t n2, uint64_t n3){
    double *packA = (double*)aligned_alloc(64, sizeof(double)*(gemm_mc+1)*gemm_kc*ncore);
    double *packB = (double*)aligned_alloc(64, sizeof(double)*(gemm_nc+1)*gemm_kc);
    printf("%d %d %d\n", n1, n2, n3);
    //js是Cj块的起始列号, Bj的起始列号
    for(uint64_t js = 0; js < n3; js += gemm_nc){
        //as是Ap块的起始列号, 也是Bpj的起始行号
        for(uint64_t as = 0; as < n2; as += gemm_kc){
            /*
            *   计算Ap*Bpj
            *   这里Cj和Ap在原矩阵中都是列块，此时访问数据的方式已变为：
            *   Cj(i,j) = C[i*ldc + offset_c + j]
            *   而B是pack过后的数据
            */  
            //is是Cij的起始行索引
            packBpj(&b[as*n3], n3, js, packB);   
            #pragma omp parallel for num_threads(ncore)      
            for(uint64_t is = 0; is < n1; is += gemm_mc){
                //计算Aip*Bpj
                //按列划分，并把Aip打包到packA
                int tid = omp_get_thread_num();
                packAip(&a[is*n2], n2, as, packA, tid);
                macro_kernel(&c[is*n3], n3, js, packA+(uint64_t)tid*gemm_mc*gemm_kc, packB);
            }
        }
    }
    free(packA);
    free(packB);
}

packB：

1
2
3
4
5
6
7
8
9
10
11
12
//将Bpj按照nr列一组，组内行优先放入packB
void packBpj(double *ob, size_t ldb, size_t offset_b, double *nb){
    #pragma omp parallel for num_threads(ncore)
    for(uint64_t j = 0; j < gemm_nc ; j += gemm_nr){	//nc/nr列
        for(uint64_t i = 0; i < gemm_kc; i++){			//kc行
            for(uint64_t k = 0; k < gemm_nr; k++){
                //将ob的第i行j列起第k个放入nb
                nb[j*gemm_kc + i*gemm_nr + k] = ob[i*ldb + offset_b + j + k];
            }
        }
    }
}

packA：

1
2
3
4
5
6
7
void packAip(double *oa, size_t lda, size_t offset_a, double *na, int tid){
    for(uint64_t i = 0; i < gemm_mc; i++){
        for(uint64_t j = 0; j < gemm_kc; j++){
            na[(uint64_t)tid*gemm_mc*gemm_kc + i*gemm_kc + j] = oa[i*lda + offset_a + j];
        }
    }
}

macro_kernel:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void macro_kernel(double *c, size_t ldc, size_t offset_c, double *a, double *b){
    //将C分为mr*nr的小块计算
    for(uint64_t i = 0; i < gemm_mc; i+=gemm_mr){
        for(uint64_t j = 0; j < gemm_nc; j += gemm_nr){
            //C00 = A(0,P)*B(P,0) C01 = A(0,P)*B(P,1) ...
            for(uint64_t ii=0; ii < gemm_mr; ii++){
                __m512d vec1 = _mm512_load_pd(&c[(i+ii)*ldc+offset_c+j]);
                __m512d vec2 = _mm512_load_pd(&c[(i+ii)*ldc+offset_c+j+8]);
                __m512d vec3 = _mm512_load_pd(&c[(i+ii)*ldc+offset_c+j+16]);
                __m512d vec4 = _mm512_load_pd(&c[(i+ii)*ldc+offset_c+j+24]);
                //i是Cij的行号, j为列号
                for(uint64_t p = 0; p < gemm_kc; p++){
                    __m512d vec_a = _mm512_set1_pd(a[(i+ii)*gemm_kc+p]);
                    __m512d vec_b1 = _mm512_load_pd(&b[gemm_kc*j+p*gemm_nr]);
                    __m512d vec_b2 = _mm512_load_pd(&b[gemm_kc*j+p*gemm_nr+8]);
                    __m512d vec_b3 = _mm512_load_pd(&b[gemm_kc*j+p*gemm_nr+16]);
                    __m512d vec_b4 = _mm512_load_pd(&b[gemm_kc*j+p*gemm_nr+24]);
                    vec1 = _mm512_fmadd_pd(vec_a, vec_b1, vec1);
                    vec2 = _mm512_fmadd_pd(vec_a, vec_b2, vec2);
                    vec3 = _mm512_fmadd_pd(vec_a, vec_b3, vec3);
                    vec4 = _mm512_fmadd_pd(vec_a, vec_b4, vec4);
                }
                _mm512_store_pd(&c[(i+ii)*ldc+offset_c+j], vec1); 
                _mm512_store_pd(&c[(i+ii)*ldc+offset_c+j+8], vec2);
                _mm512_store_pd(&c[(i+ii)*ldc+offset_c+j+16], vec3);
                _mm512_store_pd(&c[(i+ii)*ldc+offset_c+j+24], vec4);
            }
        }
    }
}

6.LOGISTIC方程

AVX512+OPENMP。一开始就直接尽量填充了流水线，如果没有这么做，可能拿不满分数。见代码。

7.H66

用Vtune可以找到热点代码是spmv，原始计算是使用COO格式完成的，可以转为CSR，然后使用AVX和OPENMP计算，只拿到了部分分数，因为时间问题，没有尝试其他压缩格式。等题解。

以下是CSR的SPMV计算过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//out=m*v;
void mmv(std::vector<double>& out, const sparse_csr& m, const std::vector<double>& v) {
    #pragma omp parallel for num_threads(ncore)
    for (auto& x : out) {
        x = 0;
    }
    /*COO SPMV
    for (size_t i = 0; i < m.data.size(); i++) {
        out[m.row[i]] += m.data[i] * v[m.col[i]];
    }
    */

    //CSR SPMV
    #pragma omp parallel for num_threads(ncore) schedule(dynamic)
    for(int i=0;i<m.nrow;i++){
        __m512d yi1 = _mm512_set1_pd(0.0);
        int start = m.row_ptrs[i], end = m.row_ptrs[i+1];
        int j;
        for(j = start; j + 8 < end; j += 8){
            __m512d m_vec1 = _mm512_loadu_pd(&m.data[j]);
            __m512d v_vec1 = _mm512_set_pd(v[m.col_idx[j+7]], v[m.col_idx[j+6]], v[m.col_idx[j+5]], v[m.col_idx[j+4]], v[m.col_idx[j+3]], v[m.col_idx[j+2]], v[m.col_idx[j+1]], v[m.col_idx[j]]);
            yi1 = _mm512_fmadd_pd(m_vec1,v_vec1,yi1);
        }
        double sum = _mm512_reduce_add_pd(yi1);
        for(; j < end; j++){
            sum += m.data[j]*v[m.col_idx[j]];
        }
        out[i] = sum;
    }
}

8.光之游戏

未完成，等题解。

9.洪水困兽

OPENMP题，对其中一部分数据要原子更新，并行化就可以拿到满分。