OpenFFT-SME-FFT算法在支持SME指令集的CPU上的实现
OpenFFT-SME: An Effcient Outer Product Pattern FFT Library on ARM SME CPUs
本篇文章来自IPDPS24,介绍了OpenFFT,一个使用ARM SME指令加速FFT运算的FFT运算库。OpenFFT SME在ARM SME CPU上的性能优于矢量化方法,与FFTW相比,在双精度下实现了3.60倍(2的幂)和4.14倍(非2的幂次)的加速,单精度下的加速为4.38倍(2的幂次)和7.02倍(非2的幂次)。
1 ARM SME指令集
矩阵乘法是人工智能负载或科学计算等多领域应用的常用计算模式,有许多加速器都是针对矩阵运算提出的,包括NVIDIA的 Tensor Core,Inter AMX。ARM的可扩展矩阵运算指令集(SME)通过提供向量外积指令来有效实现矩阵乘法,SME基于SVE构建,针对矩阵工作负载,还引入了ZA矩阵寄存器来存储矩阵数据,以及在寄存器和存储器之间加载、存储和传输矩阵的指令。
SME 引入了 Streaming SVE 模式,高吞吐处理数据,大多数SME指令都仅在该模式下使用。在Steaming SVE模式,有Z0-Z31向量寄存器,和15个Predicate寄存器。
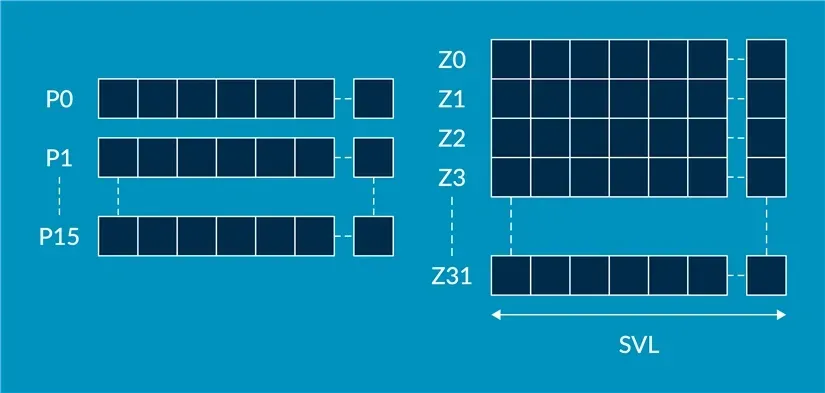
SME 新引入的 ZA array是一个二维正方形数组,大小是 SVL x SVL。行和列的长度和Zn寄存器一致。ZA array的每一行都可以当成一个SVL长度的向量来访问。而ZA array又可划分为ZA tile,ZA tile的宽度是SVL,ZA可分成多少个可用的ZA tile由元素数据类型大小决定,例如SVL是32字节,则ZA Array是32×32的,对于8bit的数据,只有一个ZA tile,对于16bit的数据,一行可存储16个数据,因此ZA tile是16×16的,ZA可分成两个ZA tile。同理,32bit的数据一行可存储8个,ZA可被划分为4个ZA tile。
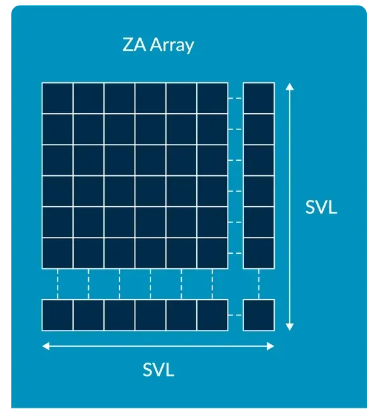
SME增加了一些新指令以及操作ZA的指令,包括:
- 矩阵外积累加/减:FMOPA、UMOPA等,SVE2向量寄存器作为外积运算输入,ZA保存结果
- SVE向量与ZA行列加法运算指令
- ZA tile的清零
- SVE向量存入或取出ZA tile的行或列的指令
假设SVL=128bit,存储FP32的向量进行SME外积运算如图所示:
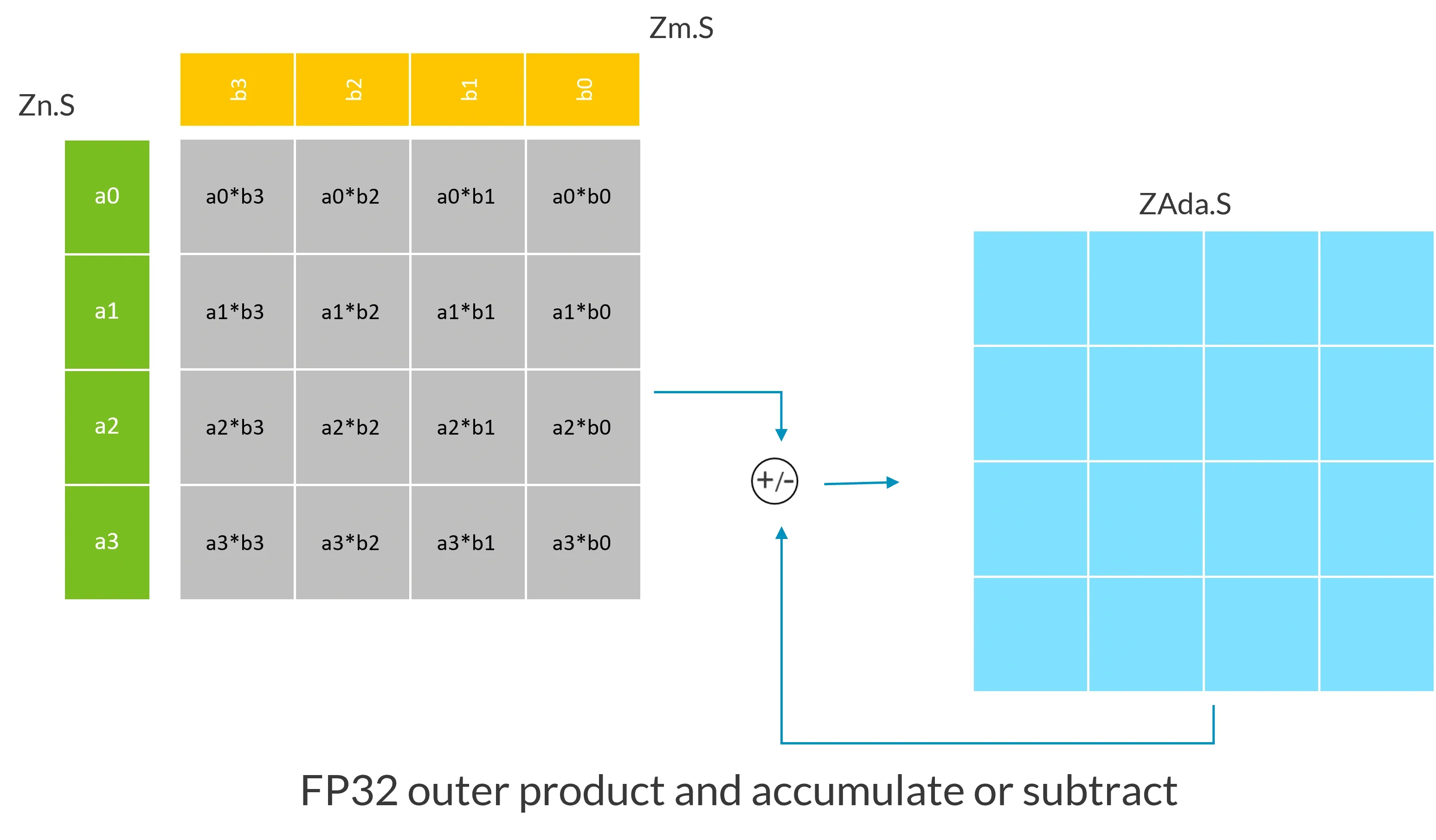
更多内容可以阅读ARM文档以及参考链接。
2 快速傅里叶算法(FFT)
点击这里查看这篇文章3 OpenFFT-SME
FFT中的蝴蝶运算本质上是矩阵向量乘法,因此ARM SME可以通过利用其外积指令来有效地加速FFT。通过自然地将蝴蝶映射到外积运算,ARM SME并行化了Cooley-Tukey FFT的计算。此外,本篇的工作还利用了旋转因子的对称和周期性质来优化计算。核心工作是:
- 实现了基于SME的FFT外积算法,并利用对称性减少外积计算
- 讨论了FFT优化的矩阵化和向量化技术,为其他算法在ARM SME上的移植提供了重要的参考价值。
3.1 外积计算的FFT算法
蝶形算法是Cooley-TukeyFFT算法的核心,优化蝶形算法是最关键的部分。因此本篇首先提出了一个外积计算FFT蝶形运算的方式,以及通过对称性减少外积计算量。
3.1.1 矩阵化运算
蝶形计算的本质是DFT矩阵与输入向量之间的乘法。即:
y和x是长度为r的复数向量,r为FFT算法的基。为了充分利用ARM SME的矩阵乘计算能力,并行计算多组蝶形计算:
Y和X是r×b的矩阵,b是并行计算的蝶形运算数量。
由于ARM SME只支持实数外积指令,所以首先要做的是将复数计算转换为一个可被计算的等价表示,我们将上式的矩阵乘使用外积形式表示:
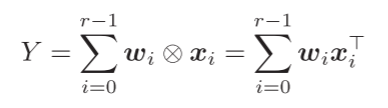
其中$w_i$是W的第i列,$x_i^T$是X的第i行。设$w_i=a_i+b_ij$以及$x_i=c_i+d_ij$,则蝴蝶计算可表示为:
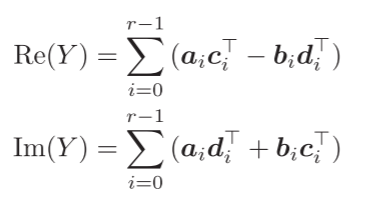
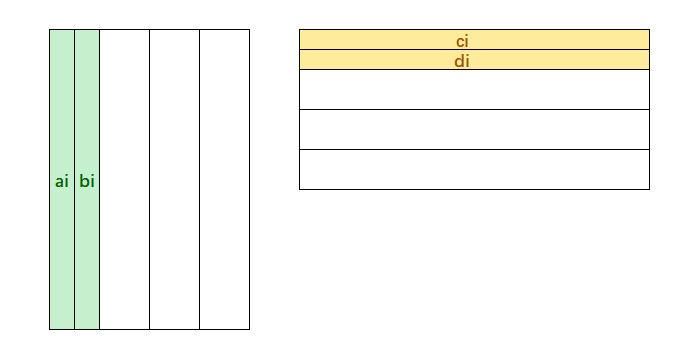
[!IMPORTANT]
后续的内容均以i表示DFT矩阵的第i列,而k则用来表示行
3.1.2 Symmetric-reduce
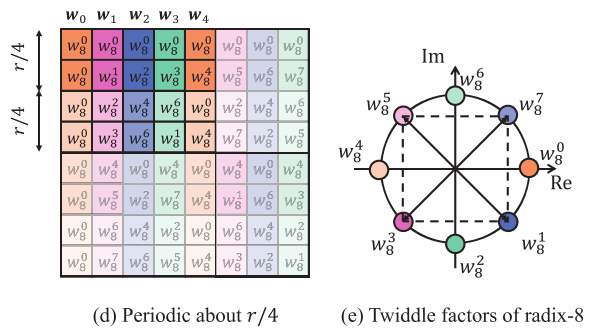
DFT矩阵具有固有的对称性,可以利用对称性提高计算效率。如图e所示,$w_i$和$w_{r-i}$是关于实轴对称的,所以有
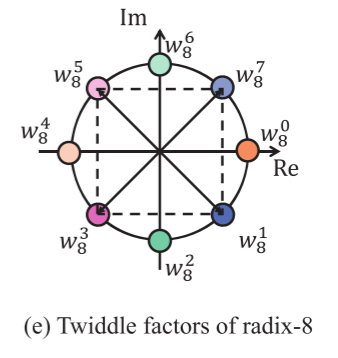
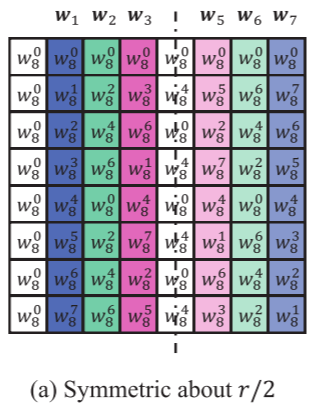
在DFT矩阵中,对称性如图a所示,相同颜色的列表示对称。
因为$b_0、b_{r/2}$是0,所以有:
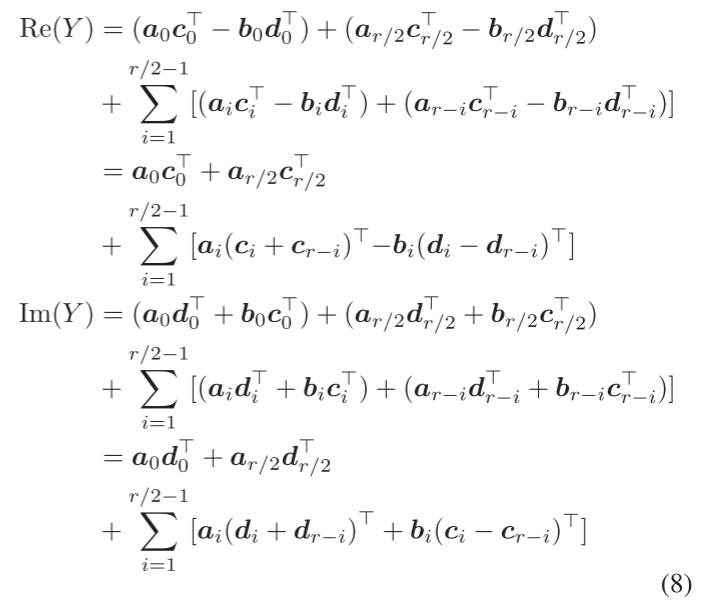
r为奇数时类似。通过对称性,可以将外积计算从4r减少到2r,只需要预先对输入向量进行一些加减运算。文章中称这样减少计算为Symmetric-reduce。
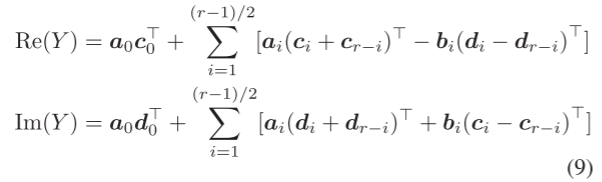
3.1.3 Periodic-reduce
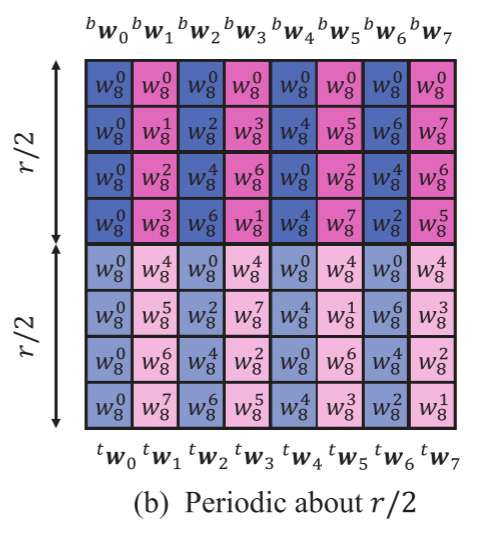
本节提出了r=2m的reduce模式,称之为periodic-reduce,利用了DFT矩阵的垂直周期性。对于偶数长度的向量或偶数行的矩阵,作者采用b(bottom)表示每行的前半部分,t(top)表示每行的后半部分。
根据旋转因子的定义,有如下的性质,上标中的i表示W的第i列,k则表示行。这个性质表示的是,对于偶数列,旋转因子在行方向上是上半下半完全相同的,而对于奇数列,上半下半的对应位置元素刚好相差$\frac r2$,是相反数。
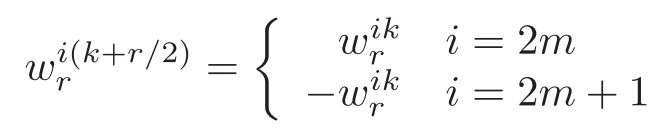
图b展现了上面的对称性,蓝色列是奇数列,上半下半完全相同,粉色列上半下半值相反。
把原来的外积计算也划分为上半和下半块,有:
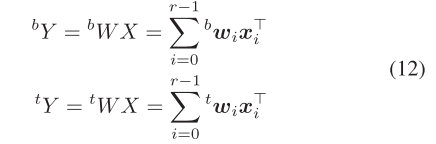

这样就把原来的外积计算转换为了W的上半和下半部分分别和X进行外积,再对外积计算划分为奇数和偶数部分,对于上半部分:

下半部分:
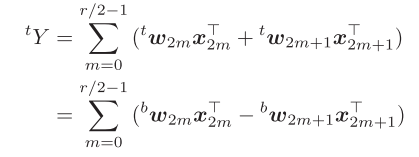
外积是一个累加操作,可以很自然的把两部分分开,对应Y的累加层:
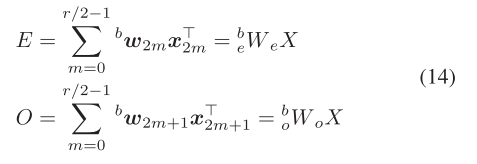
这样就将Y=WX的外积计算通过划分为两部分,利用了周期性减少了内存访问,非常巧妙:

通过上述等式,计算可以分为两步,首先计算外积的偶数和奇数部分获取矩阵E和O,然后通过对Y的上半及下半分别采用加法和减法合并,从而减少了外积的内存访问。
上述的两种方法是正交的,因此可以在使用Periodic的基础上在行内使用Symmetric-reduce。并且还可以发现,偶数列的W和$\frac r2$的DFT是等价的,所以可以转换为$\frac r2$的DFT蝶形计算,因此矩阵E的计算可以递归分解,直到r是奇数。
3.1.4 向量寄存器重用
利用上面的对称性,论文提出了向量寄存器重用模式。
根据图e的对称特性,当r=2m时,可以总结出如下的对称性,从而能进行寄存器复用,可以对照图c理解。为了方便记忆,可以记为水平方向上的寄存器重用。

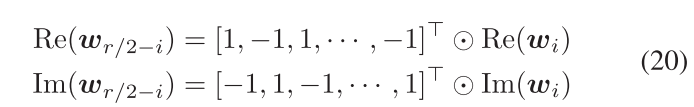
从周期性的角度,如果r是4m+4,则可以提出如下的性质,即对于不同的列,列内有关于r/4的对称性,可参考图e和d。例如对于第一列,$W_8^1=a+bi$,而$W_8^3=b-ai$。从而可以做到外积寄存器重用。可记为垂直方向上的寄存器重用。
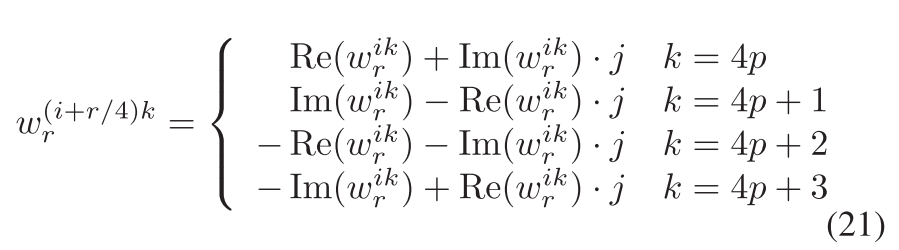
3.1.5 外积计算模式
根据上述的对称性,论文提出了优化后的外积模式。
- r为奇数:只使用Symmetric-reduce
- r为偶数:如果r小于vl,只使用Symmetric-reduce,否则同时使用两种对称性
计算数量的约减如表1所示:
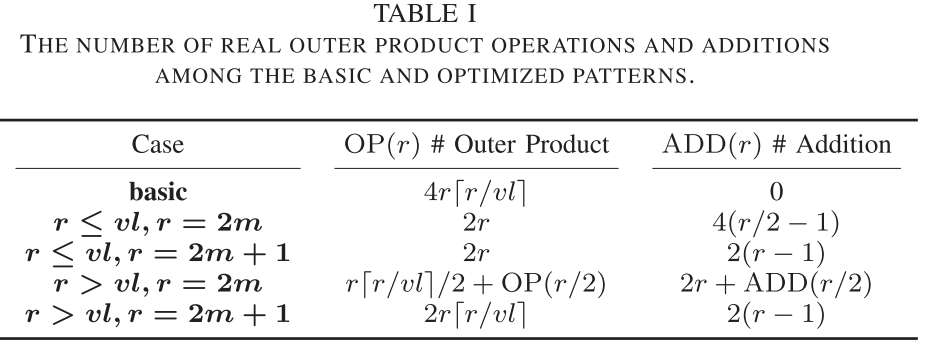
按照表中的顺序,5种case的计算量为:
- case basic:r/vl完成外积,共r组,实部虚部需要4次计算
- case 1:在basic的基础上,通过行方向的对称性减少了一半的外积计算,引入了c和d的四种(r/2-1)的加法运算
- case 2:case 1的基础上,减少了一个加法
- case 3:在case 2的基础上,可以做列上的对称性缩减计算,外积计算长度减半,加上向量寄存器重用,实部虚部可复用,计算量再次减半,外积计算递归约减为了OP(r/2)以及引入的ADD(r/2)
- case 4:和case2一致,只是外积计算需要多次完成
3.1.6 外积FFT Kernel
本节中,作者首先提出了基本实现,然后讨论了优化后的外积模式的实现问题,最后介绍了在kernel中的软件流水线优化。
基本实现
图2显示了外积模式蝶形计算的基本实现,将蝶形计算视为矩阵化运算一节已说明的实部虚部分离的外积公式。Z0,Z1,Z2,Z3都是向量寄存器,分别从DFT矩阵的实部和虚部加载数据,然后执行fmopa指令,累加到输出的实部与虚部的ZA0和ZA1寄存器。
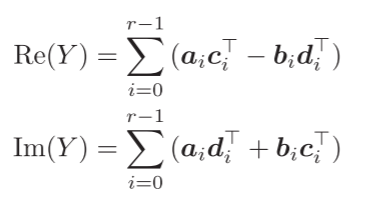
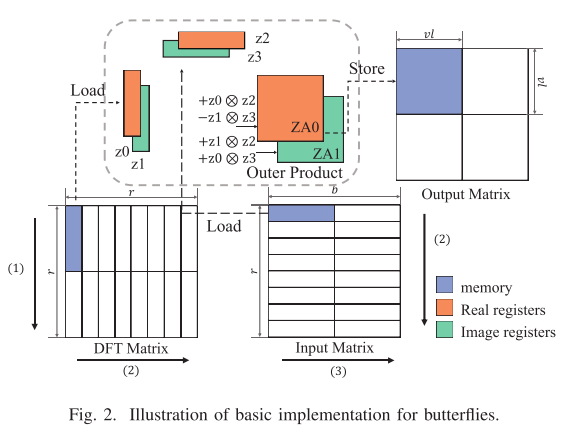
优化实现
优化实现是根据外积计算模式一节所展示的4中case分别实现的,根据r和向量寄存器长度vl,采用不同的优化实现。如图3所示。
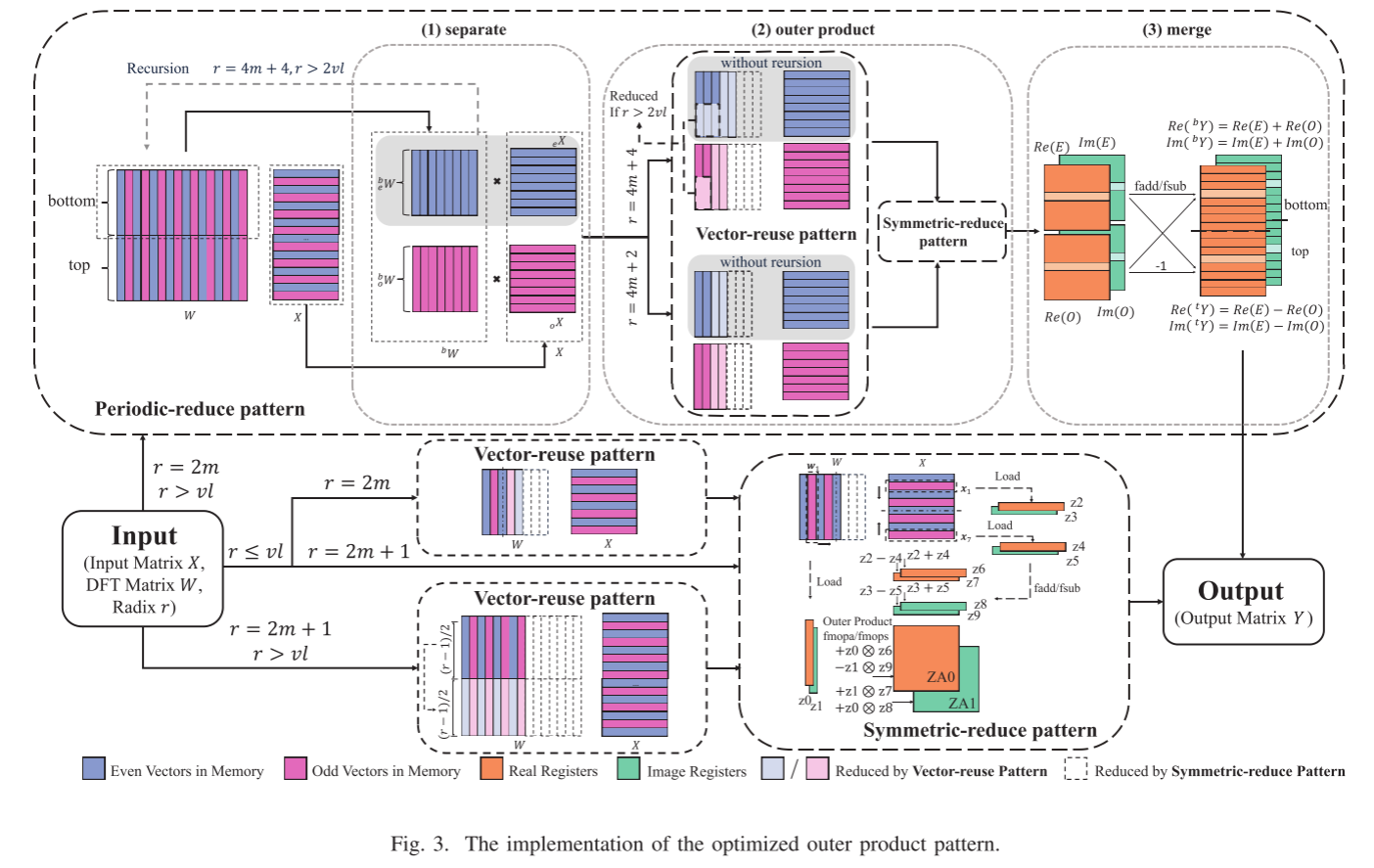
虽然在上面已经有了描述,此处还是再次说明每种情况采用哪种情况:
- $r\leq vl$:这个case中,每个向量寄存器都足够完成一列元素的加载,进行外积计算,所以仅使用水平方向的对称性Symmetric reduce来减少计算,以radix=8为例,列向量关于$w_4$对称,$w_0$和$w_4$直接进行外积计算,而$w_7、w_6、w_5$不需要进行外积计算。与基本实现相比,该模式使用了四个延迟更低,吞吐量更高的fadd/fdub替换了外积乘积。并且fadd/和fsub之间并没有数据依赖性。当r=2m时,还可以使用寄存器重用的方式,将DFT矩阵的列$i$转换到$\frac r2 - i$列,对实部使用[0,1,0,…,1]的掩码取负,对虚部使用[1,0,1,…,0]的掩码取负,以对应他们关于$\frac r4$的实部[1,-1,1…,-1]的关系,虚部[-1,1,-1…,1]的关系。
- $r\ge vl,r=2m$:这种情况可以使用垂直方向的Periodic reduce,所以第一步就是将DFT矩阵分解为奇数和偶数的部分。然后分别进行外积计算,在这个过程中可以利用水平方向寄存器重用,如果r=4m+4而且r$\gt 2vl$,可以只读取前$\frac r4$的寄存器行,根据式21来计算。
- $r \gt vl, r=2m+1$:r是奇数,垂直方向上只可使用寄存器重用,水平方向上可以采用Symmtric reduce,但是r是奇数所以不能采用水平方向的寄存器重用。
软件流水线优化
在作者的实现当中,完全展开了图2中的循环(1)和(2),只在循环(3)上做循环。当前面描述的约减模式不能使用时,可能会因为SME的高延迟和低吞吐,以及数据的依赖导致相当大的流水线停顿。
为了解决这个问题,每次循环时存储上一次迭代的结果,再为下一次迭代加载数据并执行计算,将结果存储与迭代加载计算交错,隐藏存储和移动指令的延迟,增强指令并行性。
3.2 EVALUATION
基于上述内核,本节对实现的OpenFFT-SME进行了性能评估。实验在GEM 5上进行。baseline为FFTE和FFTW,FFTE支持SVE但仅限于双精度,FFTW性能强大但只支持NEON向量化。OpenFFT为单精度和双精度都实现了基为3-16的内核,并未双精度专门实现了基为32和64的内核。
对维度为1,长度为N的FFT进行测量,性能指标为GFLOPC,将执行时间替换为周期,因为模拟器只能测量周期。
图4比较了FFTE,FFTW,OpenFFT的性能:
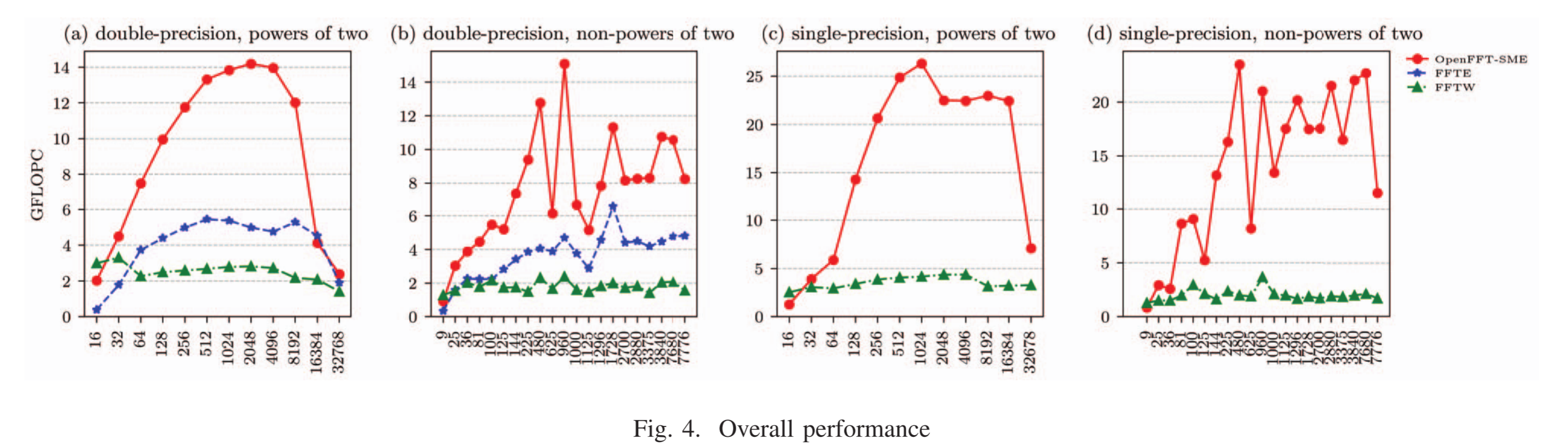
- 这些库都表现出类似的性能趋势,数据足以驻留在缓存中时,性能随数据规模提高,当FFT规模超出缓存大小时,性能降低。
- OpenFFT展现出了显著的优越性能,下表给出了加速比:
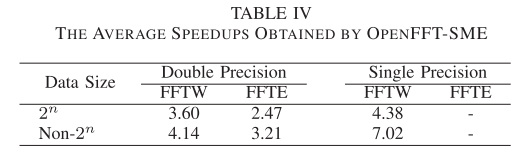
FFTW在一些小尺寸点上的显著更高的性能可能是由于特定的优化。
与向量化相比,矩阵化通过外积更好地处理稠密计算。然而,主要用于向量化的乘法和加法指令由于其轻量级性质而具有更高的计算优化潜力,所以SME没有实现ARM SME外积指令的理想性能优势。